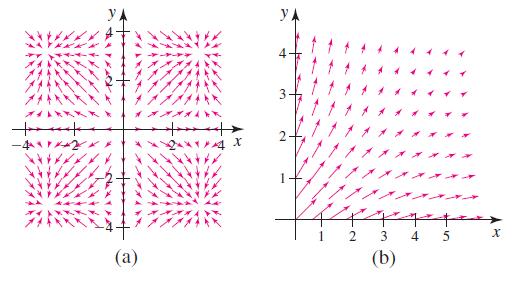
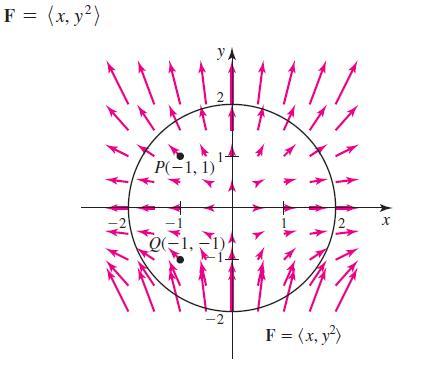
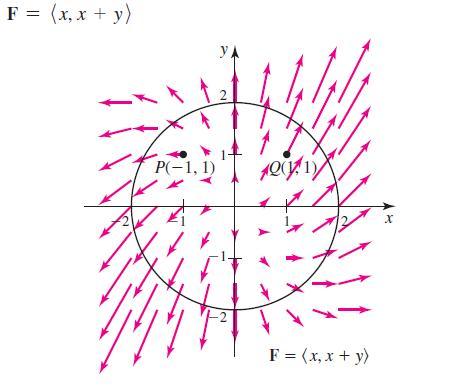
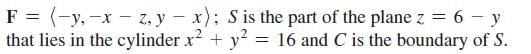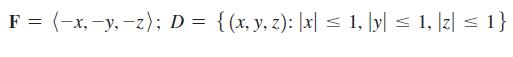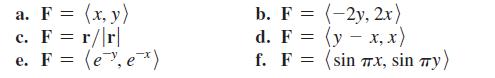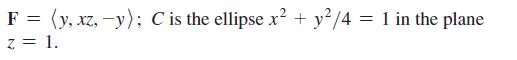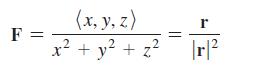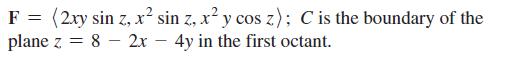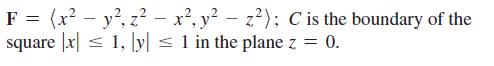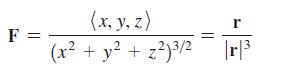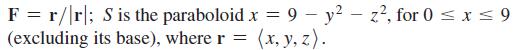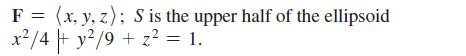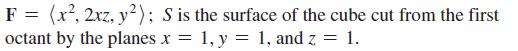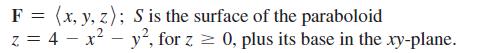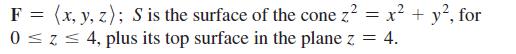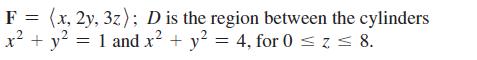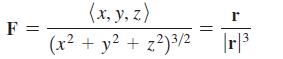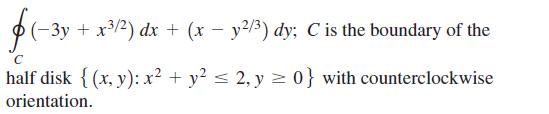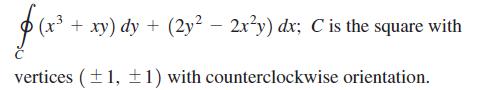Calculus For Scientists And Engineers Early Transcendentals 1st Edition William L Briggs, Bernard Gillett, Bill L Briggs, Lyle Cochran - Solutions

Unlock the full potential of "Calculus For Scientists And Engineers Early Transcendentals 1st Edition" with our comprehensive resources. Access online answers key and solutions PDF for solved problems, providing step-by-step answers to all textbook questions. Explore our detailed chapter solutions and test bank for thorough understanding. Our instructor manual offers additional insights, perfect for educators and learners alike. Discover a vast collection of questions and answers, ensuring you're well-prepared for any challenge. Enjoy the benefits of our solution manual, available for free download, enhancing your calculus journey effortlessly.