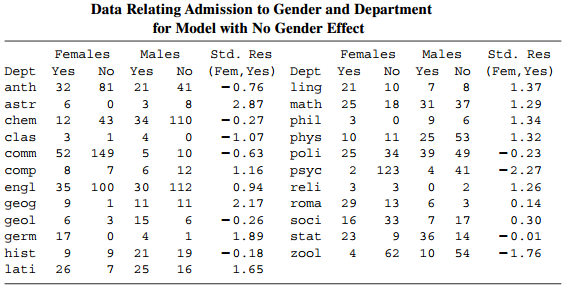
For Table 6.7 on admissions decisions for graduate school applicants, let y_ig= 1 denote a subject in department i of gender g (1 = females, 0 = males) being admitted.

a. For the fixed effects model, logit[P(Y_ig = 1)] = α + βg + β_i^D, β̂ = 0.137 (SE = 0.112). Interpret.

b. The corresponding model (12.12) in which departments are a normal random effect has β̂ = 0.163 (SE = 0.111). Interpret.

c. The model of form (12.12) allowing the gender effect to vary by department has β̂ = 0.176 (SE = 0.132), with σ̂_b = 0.20. Interpret. Explain why the standard error of β̂ is slightly larger than with the other analyses.

d. The marginal sample log odds ratio between gender and whether admitted equals €“ 0.07. How could this take different sign from β̂ in these models?

e. The sample conditional odds ratios between gender and whether admitted vary between 0 and ˆž. By contrast, predicted odds ratios for the interaction random effects model do not vary much. Explain why results can be so different.

Table 6.7:

Transcribed Image Text:

Data Relating Admission to Gender and Department for Model with No Gender Effect Females Males Std. Res Females Males Std. Res Dept Yes Yes (Fem, Yes) Dept Yes ling 21 (Fem, Yes) No No No Yes No anth 1.37 32 81 21 41 -0.76 10 math 25 astr 2.87 18 31 37 1.29 phil phys poli chem 12 -0.27 43 34 110 9. 1.34 clas -1.07 10 11 25 53 1.32 52 149 10 -0.63 25 34 39 49 -0.23 comm 12 1.16 123 -2.27 psyc reli comp engl 35 100 30 112 0.94 1.26 11 11 2.17 29 13 0.14 geog roma geol soci 16 17 6. 15 -0.26 33 0.30 17 1.89 stat 23 36 14 -0.01 germ hist zool 9. 9. 21 19 -0.18 62 10 54 -1.76 lati 26 25 16 1.65