Refer to Problem 3.27. The sample size may need to be quite large for the sampling distribution of to be approximately normal, especially if

Refer to Problem 3.27. The sample size may need to be quite large for the sampling distribution of γ̂ to be approximately normal, especially if |γ| is large. The Fisher-type transform ξ̂ = 1/2 log[(1 + γ̂)/(1 − γ̂)] converges more quickly to normality.

a. Show that the asymptotic variance of ξ̂ equals the asymptotic variance of γ̂ multiplied by (1 − γ²)^?2.

b. Explain how to construct a confidence interval for ξ and use it to obtain one for γ.

c. Show that ξ̂  = 1/2 log(C/D). For 2 × 2 tables, show that this is half the log odds ratio.

Data from Problem 3.27:

For ordinal variables, consider gamma (2.14). Let

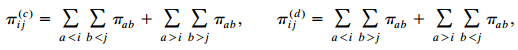
Where i and j are fixed in the summations. Show that II_c = ∑_i ∑_j π_ij π^(c)_ij and II_d = ∑_i ∑_j π_ij π^(d)_ij. Use the delta method to show that the large-sample normality (3.9) applies for γ̂ , with (Goodman and Kruskal 1963)

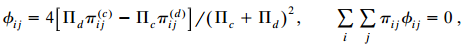
a j + a j a>i b