Refer to Problem 3.42 and exact tests using X²with Hα: Ï€₁‰  Ï€₂. Explain why the unconditional P-value, evaluated at Ï€ = 0.5, is related to Fisher conditional P-values for various tables by 

Thus, the unconditional P-value of 1/32 is a weighted average of the Fisher P-value for the observed column margins and P-values of 0 corresponding to the impossibility of getting results as extreme as observed if other margins had occurred i.e.

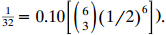
The Fisher quote in Section 3.5.6 gave his view about this.

Data from Prob. 3.42:

A contingency table for two independent binomial variable has counts (3, 0 / 0, 3) by row. For H₀: Ï€₁ = Ï€₂ and H_α : Ï€₁ > Ï€₂, show that the P-value equals 1/64 for the exact unconditional test and 1/20 for Fisher€™s exact test.

P(X > 6) = E P(X > 6 +1 = k)P(n+ = k) . k=0 - 0.10 (8)(1/2)*), %3D 32