We have the following properties for a certain mixture for mixing at constant temperature and pressure: 

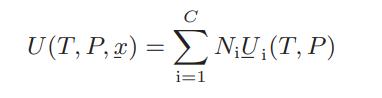
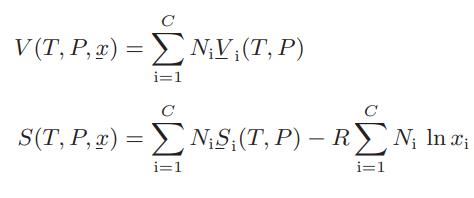
where S_i, the pure-component molar entropy of component i, is given by

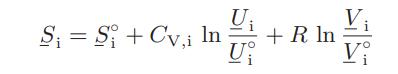 Here S°_i , U°_i , and V°_i are the molar entropy, internal energy, and volume of pure component i in some reference state, and C_V,_i is its constant-volume heat capacity.

a. Obtain expressions for the partial molar volume, partial molar internal energy, partial molar entropy, and partial molar Gibbs energy of each component in this mixture in terms of S°_i , U°_i , V°_i , C_V,i, R, and T. 

b. Obtain expressions for the volumetric and thermal equations of state for this mixture. 

c. Obtain expressions for the enthalpy and the Helmholtz and Gibbs energies of this mixture. 

Transcribed Image Text:

C U(T, P, x) = ΣN₁U¡(T, P) i=1