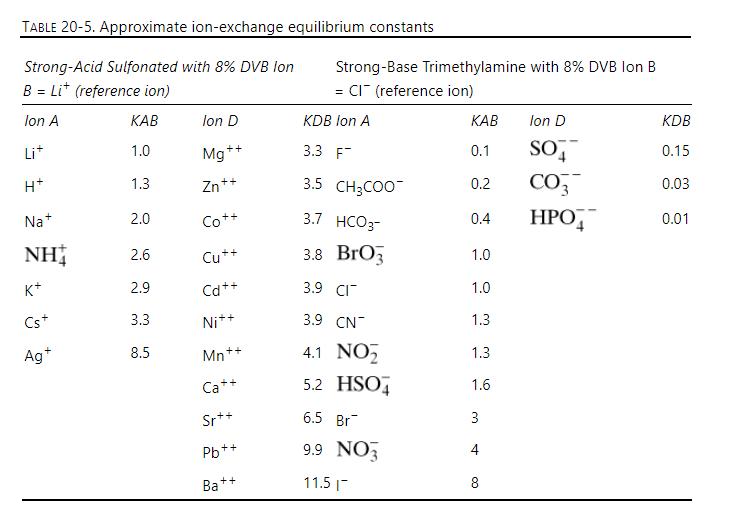
A column packed with a strong cation exchanger is initially in the \(\mathrm{K}^{+}\)form, \(\mathrm{c}_{\mathrm{T}}=0.020\) eq/L. The column is \(75.0 \mathrm{~cm}\) long, superficial velocity is \(20.0 \mathrm{~cm} / \mathrm{min}\), and flow is in same direction for all steps, \(\varepsilon_{\mathrm{p}}=0, \varepsilon_{\mathrm{e}}=0.40, \mathrm{~K}_{\mathrm{E}}=1.0\) (cations), and \(\mathrm{c}_{\mathrm{RT}}=2.0 \mathrm{eq} / \mathrm{L}\). Equilibrium data are in Table 20-5.

a. At \(\mathrm{t}=0\), feed column with a solution with \(\mathrm{c}_{\mathrm{T}}=0.020 \mathrm{eq} / \mathrm{L}, \mathrm{x}_{\mathrm{Ca}}=0.80, \mathrm{x}_{\mathrm{K}}=0.20\). Plot outlet value of \(\mathrm{x}_{\mathrm{Ca}}\) vs. time.

b. At \(\mathrm{t}=500 \mathrm{~min}\), column is regenerated with a pure aqueous solution of \(\mathrm{K}^{+}\)with \(\mathrm{x}_{\mathrm{K}}=\) \(1.0, \mathrm{x}_{\mathrm{Ca}}=0.0\), and \(\mathrm{c}_{\mathrm{T}}=1.0 \mathrm{eq} / \mathrm{L}\). Plot outlet values of \(\mathrm{c}_{\mathrm{T}}\) and \(\mathrm{x}_{\mathrm{Ca}}\) vs. time.

c. As an alternative regeneration procedure, at \(\mathrm{t}=500\) minutes, regenerate with a pure aqueous solution of \(\mathrm{K}^{+}\)with \(\mathrm{x}_{\mathrm{K}}=1.0, \mathrm{x}_{\mathrm{Ca}}=0.0\), and \(\mathrm{c}_{\mathrm{T}}=1.40 \mathrm{eq} / \mathrm{L}\). Plot outlet \(\mathrm{c}_{\mathrm{T}}\) and \(\mathrm{x}_{\mathrm{Ca}}\) vs. time.

If any of these steps require you to calculate a diffuse wave, calculate velocities and breakthrough times at three values of \(\mathrm{x}_{\mathrm{Ca}}\) : at highest and lowest mole fractions and at \(\mathrm{x}_{\mathrm{Ca}}\) \(=0.50\).

TABLE 20-5. Approximate ion-exchange equilibrium constants Strong-Acid Sulfonated with 8% DVB lon B = Lit (reference ion) Strong-Base Trimethylamine with 8% DVB Ion B = CI (reference ion) Ion A KAB Ion D KDB Ion A KAB lon D KDB Li+ 1.0 ++ Mg 3.3 F 0.1 SO 0.15 H+ 1.3 Zn++ 3.5 CH3COO 0.2 CO3 0.03 Na+ 2.0 Co++ 3.7 HCO3- 0.4 HPO 0.01 NH 2.6 Cu++ 3.8 Bro 1.0 K+ 2.9 Cd++ 3.9 CI Cs+ 3.3 Ni++ 3.9 CN 1.3 13 1.0 Ag+ 8.5 Mn++ 4.1 NO 1.3 Ca++ 5.2 HSO 1.6 36 Sr++ 6.5 Br 3 Pb+ ++ 9.9 NO 4 Ba++ 11.5 8