A slurry of pure \(\mathrm{NaCl}\) crystals, \(\mathrm{NaCl}\) in solution, \(\mathrm{NaOH}\) in solution, and water is sent to a system of thickener(s) at a rate of \(100.0 \mathrm{~kg} / \mathrm{min}\). The feed slurry is \(45.0 \mathrm{wt} \%\) crystals. The mass fractions of the entire feed (including crystals and solution) are \(\mathrm{x}_{\mathrm{NaCl}}=0.5193, \mathrm{x}_{\mathrm{NaOH}}=0.099\), and \(\mathrm{x}_{\text {water }}=\) 0.3187 . Remove \(\mathrm{NaOH}\) by washing with a saturated \(\mathrm{NaCl}\) solution. Thickener(s) are operated so that underflow is \(80.0 \%\) solids (crystals) and \(20.0 \%\) liquid. There are no solids in the overflow. Solubility of \(\mathrm{NaCl}\) in caustic solutions ( \(\mathrm{y}\) value) is listed in following table (Brown et al., 1950). The first two rows of \(\mathrm{x}\) values (weight fraction in underflow including both crystals and solution) have been calculated so that you can check your calculation procedure. The \(\mathrm{x}\) values are specific for this operation in which the underflow is \(80.0 \%\) solids, and the crystals are pure \(\mathrm{NaCl} .\left[\mathrm{x}_{\mathrm{NaCl}}=\right.\) \(\left.0.8(1.0)+0.2 \mathrm{y}_{\mathrm{NaCl}}, \mathrm{x}_{\mathrm{NaOH}}=0.8(0)+0.2 \mathrm{y}_{\mathrm{NaOH}}\right]\)

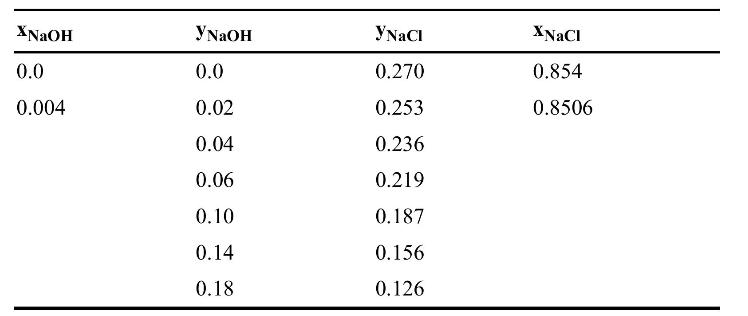
a. Complete the table, plot the saturated extract (y) and saturated raffinate (x) curves, and construct a conjugate line.
b.* If the feed is mixed with \(20.0 \mathrm{~kg} / \mathrm{min}\) of a saturated \(\mathrm{NaCl}\) solution ( \(\mathrm{y}_{\mathrm{NaCl}}\) \(\left.=0.27, \mathrm{y}_{\mathrm{NaOH}}=0.0\right)\) in a single thickener, find the flow rates of the underflow and the overflow, the compositions of these streams, and the weight of the crystals in the underflow. *Partial answer in part d.

c. If a countercurrent cascade of thickeners is used with \(S=20.0 \mathrm{~kg} / \mathrm{min}\) of a saturated \(\mathrm{NaCl}\) solution \(\left(\mathrm{y}_{\mathrm{NaCl}}=0.27, \mathrm{y}_{\mathrm{NaOH}}=0.0\right)\) and we desire a raffinate product that has \(\mathrm{x}_{\mathrm{NaOH}}=0.01\), determine the flow rates of \(\mathrm{R}_{1}\) and \(\mathrm{E}_{\mathrm{N}}\) and the number of stages required.

d. Raffinate from part \(\mathrm{b}, \mathrm{R}_{1}=56.63 \mathrm{~kg} / \mathrm{min}, \mathrm{x}_{\mathrm{R} 1, \mathrm{NaCl}}=0.833\), is mixed in a second stage with fresh solvent, which makes this a crossflow system. The goal is to have raffinate from the second stage have \(\mathrm{x}_{\mathrm{R} 2, \mathrm{NaOH}}=1.0 \mathrm{wt} \%\). Find the flow rate of the solvent that has to be added, the flow rates of \(\mathrm{R}_{2}\) and \(\mathrm{E}_{2}\), and the compositions of \(\mathrm{R}_{2}\) and \(\mathrm{E}_{2}\).
Note: Although this is a washing problem, there is not a constant flow rate of solids. Thus, it needs to be solved like the leaching problems in this chapter.

Transcribed Image Text:

XNaOH YNaOH YNACI XNaCl 0.0 0.0 0.270 0.854 0.004 0.02 0.253 0.8506 0.04 0.236 0.06 0.219 0.10 0.187 0.14 0.156 0.18 0.126