Derive the solutions for transient concentration profiles in the two-bulb apparatus (Example 21.5 in the text) for the binary case, and show that the multicomponent case can be derived as an extension of this. What assumption is implicit in extending the binary case to the multicomponent case?

Example 21.5:

Two bulbs containing gas mixtures with different compositions at time zero are connected by a porous plug, and transient diffusion is allowed to occur. First we analyze the binary diffusion and then show how the results may be generalized for a multicomponent system based on the linear model.

The binary solution is
y_i − y_i∞ = (y_i0 − y_i∞)exp(−βDt)
where β is the cell constant and D is the binary diffusivity. This was indicated in Problem 6 of Chapter 10, using the pseudo-steady-state hypothesis.
The multicomponent solution is simply the vector extension of this result: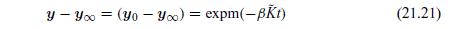

where the expm is the matrix exponential of the matrix term within the brackets.We show the results for a gas mixture of hydrogen, nitrogen, and carbon dioxide.The initial composition in bulb 1 was chosen to be 0.5 for nitrogen and 0.5 for carbon dioxide.The initial composition in bulb 2 was chosen to be 0.5 for nitrogen and 0.5 for hydrogen.The K matrix was computed for a pressure of 100 kPA and a temperature of 298 K. The composition profile can then be computed directly with Eq. (21.21).
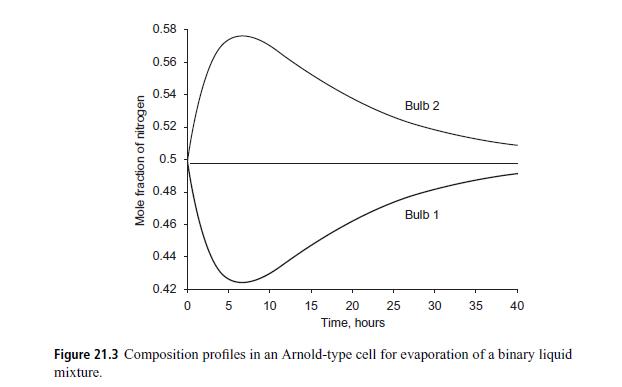
The calculated results for the composition profile of nitrogen are shown in Fig. 21.3.This shows some interesting behavior. During the early stage of the transient process nitrogen accumulates in the right bulb (bulb 2). This is an example of reverse diffusion. After some accumulation, the nitrogen diffuses back from bulb 2 to bulb 1. In the absence of diffusional interactions, there would not be any concentration profile for nitrogen, and the mole fractionin both bulbs would remain at the initial value of 0.5. The experimental data from Duncan and Toor (1962) (not shown here) are in complete conformity with these findings.

Problem 6:

Two bulbs are connected by a straight tube of diameter \(0.001 \mathrm{~m}\) and length \(0.15 \mathrm{~m}\). Initially one bulb contains nitrogen and the bulb at the other end contains hydrogen. The system is maintained at a temperature of \(298 \mathrm{~K}\) and a total pressure of \(1 \mathrm{~atm}\). The volume of each bulb is \(8 \times 10^{-6} \mathrm{~m}^{3}\).
Calculate and plot the mole-fraction profile of nitrogen in the first bulb as a function of time. Verify the validity of the quasi-steady-state approximation by calculating the diffusion time and the process time constants.

Transcribed Image Text:

y - Yo (Yo-Yoo) expm(-BKt) = (21.21)