Determine steam and water operating costs per year and TAC for the distillation system described in Problems 11.D1 and 11.D2. Use 8000 h/year. Payback period is 3 years, and costs are based on 2020 costs. What fraction of the TAC is due to energy costs?

a. Use values from Turton et al. (2018) in Table 11-9.

b. Use values from Luyben (2013) in Table 11-9 (use Turton et al. water cost).

Problem 11.D1.

Repeat Example \(11-1\) except at \(400.0 \mathrm{kPa} . \mathrm{F}=1000.0 \mathrm{lb} \mathrm{mol} / \mathrm{h}, \mathrm{L} / \mathrm{D}\) \(=4.0\), distillate is \(99.9 \mathrm{~mol} \% \mathrm{n}\)-hexane, and bottoms is \(0.1 \mathrm{~mol} \% \mathrm{n}\) hexane. At this pressure, \(\mathrm{E}_{\mathrm{o}}\) is determined in Problem 10.D1, the relative volatility depends on pressure, and diameter is calculated in Problem 10.D5. Hint: See answers to problems 10.D1 and 10.D5 in back of book immediately before the index.

a. Find \((\mathrm{L} / \mathrm{D})_{\min }\).

b. Find \(_{N \text { min }}\).

c. Estimate \(\mathrm{N}_{\text {equil }}\).

\section*{d. Estimate \(\mathrm{N}_{\text {actual }}\).}

e. Find cost of shells and trays using the bare module cost calculation procedure and the data in Table 11-2. Update costs to 2020.

Example 11-1

Example 11-2

Example 11-3

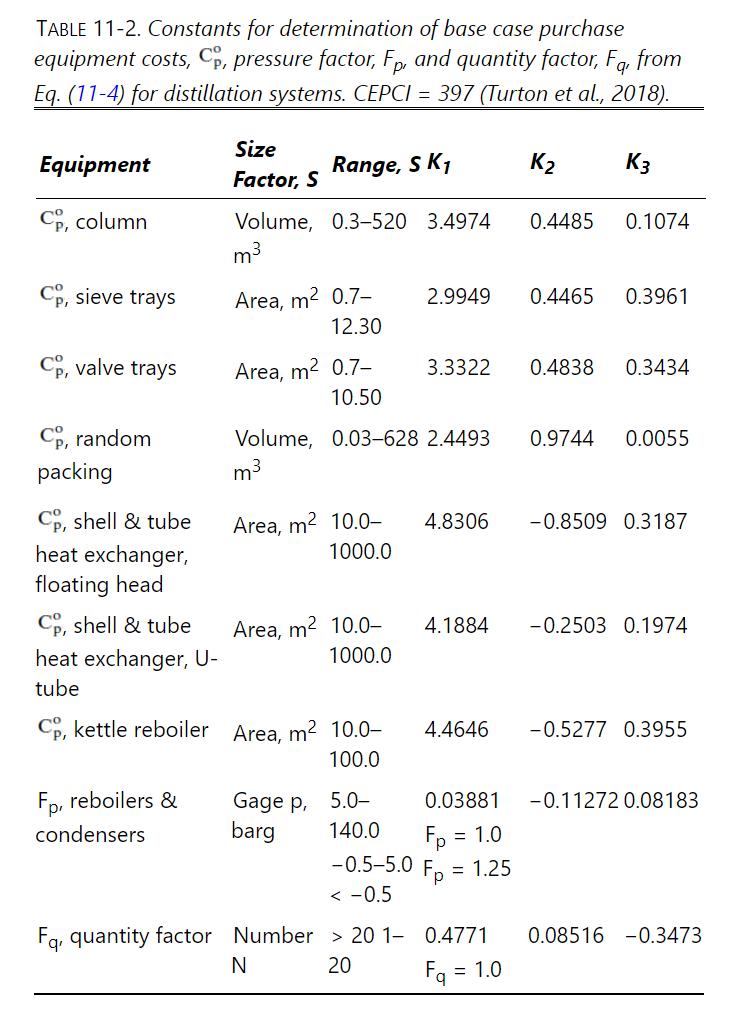
Table 11-2

Data From Problem 10.D1

Repeat Example 10-1 for an average column pressure of \(400.0 \mathrm{kPa}\).

Example 10-1

Data From Problem 10.D5

Repeat Example 10-2 except calculate the diameter at the bottom of the column at a pressure of \(400.0 \mathrm{kPa}\). The surface tension of pure \(\mathrm{n}-\) heptane at \(20^{\circ} \mathrm{C}\) is 20.14 dynes \(/ \mathrm{cm}(0.0214 \mathrm{~N} / \mathrm{m})\), and the temperature coefficient is \(-0.0980 \mathrm{dynes} / \mathrm{cm} / \mathrm{K}\) (www.surface-tension.de). Use the DePriester chart to estimate bottoms temperature.

Example 10-2

Example 10-1

Data From Problem 11.D2.

Estimate the 2020 cost of the condenser and the reboiler (shell and tube, floating head) for Problem 11.D1. Steam is available at 41.0 barg, but due to pressure losses, the steam is at \(230.0^{\circ} \mathrm{C}\) when it enters the reboiler. Cooling water is available at \(30.0^{\circ} \mathrm{C}\) and is returned to the cooling tower at \(45.0^{\circ} \mathrm{C}\). Latent heat of \(\mathrm{n}\)-hexane and \(\mathrm{n}\)-heptane can be estimated from (Green and Perry, 2008, 2-152):

\(\lambda_{\mathrm{C} 6}(\mathrm{~kJ} / \mathrm{kmol})=45,440\left(1-\mathrm{T} / \mathrm{T}_{\mathrm{c}}\right)^{0.39002}, \mathrm{~T}\) in \(\mathrm{K}, \mathrm{T}_{\mathrm{c}}=\) critical temp. \(=507.6 \mathrm{~K}\)

\(\lambda_{\mathrm{C} 7}(\mathrm{~kJ} / \mathrm{kmol})=50,014\left(1-\mathrm{T} / \mathrm{T}_{\mathrm{c}}\right)^{0.38795}, \mathrm{~T}\) in \(\mathrm{K}, \mathrm{T}_{\mathrm{c}}=\) critical temp. \(=540.2 \mathrm{~K}\)

Boiling points can be estimated from the DePriester charts.

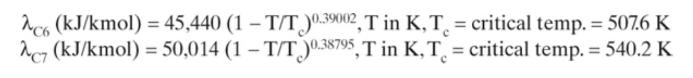
Problem 11.D1.

Repeat Example \(11-1\) except at \(400.0 \mathrm{kPa} . \mathrm{F}=1000.0 \mathrm{lb} \mathrm{mol} / \mathrm{h}, \mathrm{L} / \mathrm{D}\) \(=4.0\), distillate is \(99.9 \mathrm{~mol} \% \mathrm{n}\)-hexane, and bottoms is \(0.1 \mathrm{~mol} \% \mathrm{n}\) hexane. At this pressure, \(\mathrm{E}_{\mathrm{o}}\) is determined in Problem 10.D1, the relative volatility depends on pressure, and diameter is calculated in Problem 10.D5. Hint: See answers to problems 10.D1 and 10.D5 in back of book immediately before the index.

a. Find \((\mathrm{L} / \mathrm{D})_{\min }\).

b. Find \(_{N \text { min }}\).

c. Estimate \(\mathrm{N}_{\text {equil }}\).

\section*{d. Estimate \(\mathrm{N}_{\text {actual }}\).}

e. Find cost of shells and trays using the bare module cost calculation procedure and the data in Table 11-2. Update costs to 2020.

Example 11-1

Example 11-2

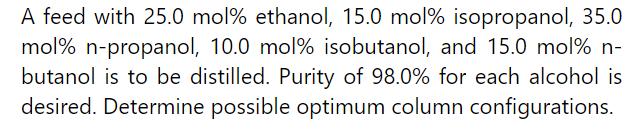
Example 11-3

Table 11-2

Data From Problem 10.D1

Repeat Example 10-1 for an average column pressure of \(400.0 \mathrm{kPa}\).

Example 10-1

Data From Problem 10.D5

Repeat Example 10-2 except calculate the diameter at the bottom of the column at a pressure of \(400.0 \mathrm{kPa}\). The surface tension of pure \(\mathrm{n}-\) heptane at \(20^{\circ} \mathrm{C}\) is 20.14 dynes \(/ \mathrm{cm}(0.0214 \mathrm{~N} / \mathrm{m})\), and the temperature coefficient is \(-0.0980 \mathrm{dynes} / \mathrm{cm} / \mathrm{K}\) (www.surface-tension.de). Use the DePriester chart to estimate bottoms temperature.

Example 10-2

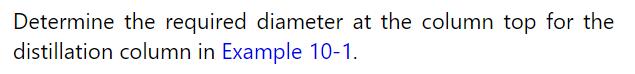
Example 10-1

Transcribed Image Text:

Estimate the cost in 2020 of the distillation column (shell and trays) designed in Examples 10-1 to 10-3. In addition, design and determine the cost of the reboiler and condenser (both shell and tube with floating head). Assume steam is at 140.0C in the reboiler, and cooling water enters at 30.0C and leaves at 45.0C. AC6 = 31,569 kJ/kmol and Ac7 = 34,676 kJ/kmol at their normal boiling points.