Develop a spreadsheet for a simple binary Rayleigh distillation that uses Eq. (9-13) but can be used for systems where \(\alpha\) is not constant. Because \(\alpha\) is not constant, calculate the values of \(\mathrm{W}_{\text {fin }, \mathrm{j}} / \mathrm{F}_{\mathrm{j}}\) over a series of relatively small ranges of \(\mathrm{x}\) using the geometric average \(\alpha\) value for each range. For example, with range \(\mathrm{j}\) from \(\mathrm{x}_{\mathrm{F}, \mathrm{j}}=0.5\) to \(\mathrm{x}_{\text {fin, } \mathrm{j}}=0.4, \alpha_{\text {avg } \mathrm{j}}=[\alpha(0.5)\) \(\alpha(0.4)]^{0.5}\) is used to calculate \(\mathrm{W}_{\text {fin }, \mathrm{j}}\). The distillate collected for period \(\mathrm{j}\) is \(\mathrm{D}_{\mathrm{j}}=\mathrm{F}_{\mathrm{j}}-\mathrm{W}_{\text {fin, } \mathrm{j}}\), and the average distillate mole fraction during period \(\mathrm{j}\) is \(x_{D, a v g, j}=\left(F_{j} x_{F, j}-W_{\text {fin, } j} x_{\text {fin, },}\right) / D_{j}\). Then for range \(j+1, F_{j+1}=W_{\text {fin }, j} \cdot x_{F, j+1}\) \(=\mathrm{x}_{\text {fin, }, \mathrm{j}}=0.4\). For \(\mathrm{x}_{\text {fin, },+1}\), pick a convenient \(\mathrm{x}\) value such as \(\mathrm{x}_{\text {fin }, \mathrm{j}+1}=0.3\), and then use \(\alpha_{\text {avg. }, j+1}=[\alpha(0.4) \alpha(0.3)]^{0.5}\) to calculate \(\mathrm{W}_{\text {fin }, j+1}\).

Equation (9-13)

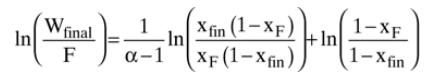
The value of \(\mathrm{D}_{\text {tot }}=\Sigma \mathrm{D}_{\mathrm{j}}=\mathrm{F}-\mathrm{W}_{\text {fin,tot }}\), and \(\mathrm{x}_{\mathrm{D}, \text { avg }}=\left(\mathrm{F} \mathrm{x}_{\mathrm{F}}-\mathrm{W}_{\text {fin,tot }}\right.\) \(\left.\mathrm{x}_{\mathrm{W}, \text { fin,tot }}\right) / \mathrm{D}_{\text {tot }}\). The individual values of \(\mathrm{x}_{\mathrm{D}, \text { avg,j }}\) are useful to check the calculation \(\left(\mathrm{x}_{\mathrm{D}, \text { avg }}=\left[\Sigma\left(\mathrm{D}_{\mathrm{j}} \mathrm{x}_{\mathrm{D}, \text { avg.j }}\right)\right] / \Sigma \mathrm{D}_{\mathrm{j}}\right)\) and whether product fractions are collected.

Solve the following problem with your spreadsheet: \(10.0 \mathrm{kmol}\) of a mixture that is \(14 \mathrm{~mol} \%\) methanol and \(86 \mathrm{~mol} \%\) water is batch distilled. Stop the batch distillation when \(\mathrm{x}_{\mathrm{W} \text {,fin }}=0.0013\) mole fraction methanol. Use the equilibrium data in Table 2-8 to calculate \(\alpha\) values. Find \(\mathrm{D}_{\text {tot }}\), \(\mathrm{W}_{\text {fin }}\), and \(\mathrm{x}_{\mathrm{D}, \text { avg }}\).

Table 2-8

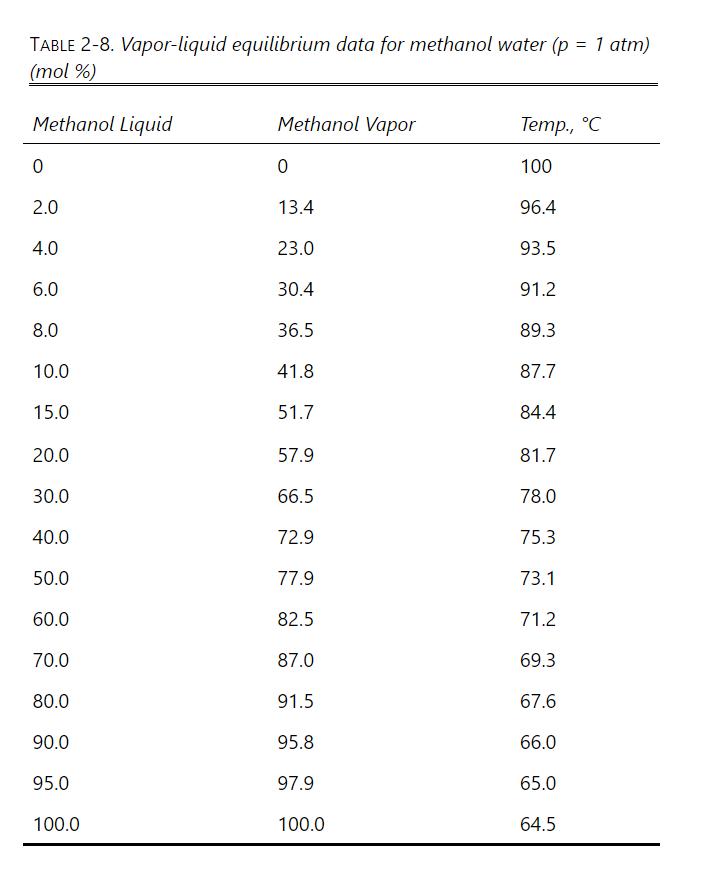
In Wfinal 1 Xfin (1-XF) 1-XF In +In F -1 XF (1-Xfin)) 1-Xfin