For the same system as in Problem 15.D1, the high concentration (mathrm{C}_{mathrm{A}, 0}=1.2 mathrm{~kg} / mathrm{m}^{3}) and
Question:
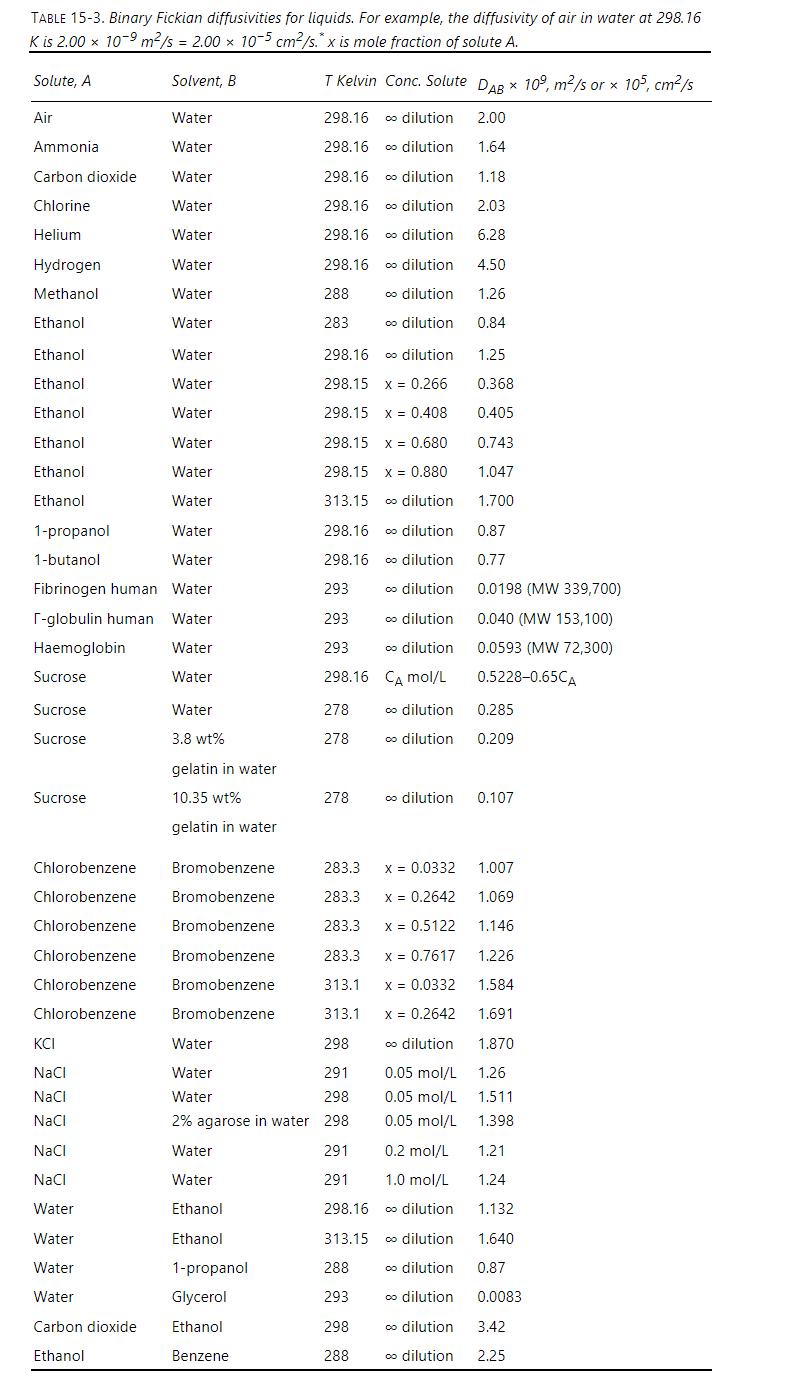
For the same system as in Problem 15.D1, the high concentration \(\mathrm{C}_{\mathrm{A}, 0}=1.2 \mathrm{~kg} / \mathrm{m}^{3}\) and \(\mathrm{C}_{\mathrm{A}, \mathrm{L}}=0.9701 \mathrm{~kg} / \mathrm{m}^{3}\), which is same as in Problem 15.D1, but we want a flux rate \(=0.35 \times 10^{-5} \mathrm{~kg} /\left(\mathrm{m}^{2} \mathrm{~s}\right)\). Apparatus temperature can be adjusted. Estimate the Fickian infinite dilution diffusivity by adjusting the value from Table 15-3 for the temperature difference by assuming that \(\mathrm{E}_{\mathrm{o}}=3000 \mathrm{cal} / \mathrm{mol}\) in Eq. \((15-22 \mathrm{c})\). What temperature is required?
Data From Problem 15.D2.
Repeat the numerical integration in Example 15-5, except use the quadrature formula, Eq. \((9-12)\)
Example 5-5

Equation (9-12)
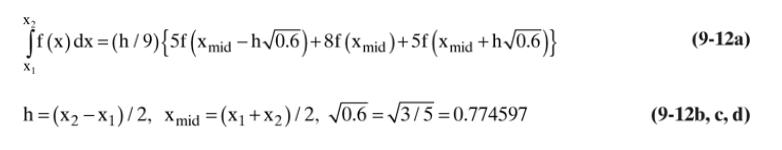
Table 15-3
Equation (15-22c)
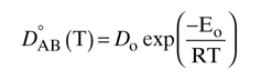
Step by Step Answer:

Separation Process Engineering Includes Mass Transfer Analysis
ISBN: 9780137468041
5th Edition
Authors: Phillip Wankat





