In analogy to the treatment in Section 5.7, derive the equations describing a countercurrent membrane reactor in
Question:
In analogy to the treatment in Section 5.7, derive the equations describing a countercurrent membrane reactor in which the reversible first-order reaction A⇄ M is carried out.
Section 5.7:
The staged systems that we have considered up to this point are realistic for many separation processes, and the large N limit provides a convenient way to analyze continuous systems. Dialysis is generally carried out continuously, and it is instructive to address the continuous system directly. The process is shown schematically in Figure 5.5. The raffinate and permeate streams flow parallel to one another in two plane channels of length L that are separated by a membrane that has a width w. (The analysis is unchanged if the membrane is a tube, except that w becomes the perimeter of the tube.) The system is countercurrent if the flows are as shown, and that is the case that we consider here. Co-current operation is also possible.
Figure 5.5:
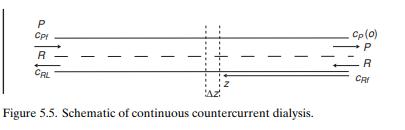
The concentration in each stream changes along the channel, so it is clear that the entire unit cannot be taken as the control volume. We choose instead a segment of each channel of length Δz, as shown in the figure; within this small region we can assume, as is typically done when using differential calculus, that the characterizing variables are constant, and we will subsequently let Δz go to zero. We assume, as before, that the amount of solute transferred between the streams is sufficiently small to allow us to take the flow rates R and P as constant in space. For this configuration we will start with the steady state in order to avoid the complication of having to deal with changes with respect to two independent variables, t and z. The steady-state mass balances in the two control volumes (raffinate side and permeate side) are then respectively.
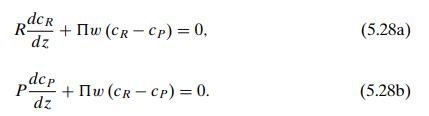

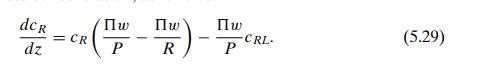
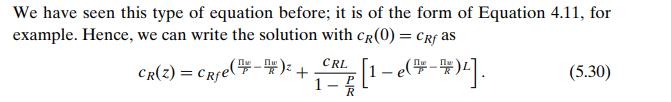

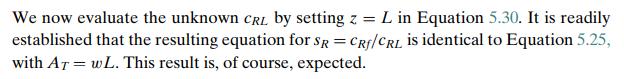
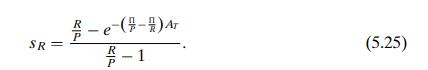
Step by Step Answer:






