Repeat Problem 10.E1, except design a packed column using 1-in. metal Pall rings. Do the calculations at the top of the column. Approximate HETP for ethanol-water is \(0.366 \mathrm{~m}\). At \(81^{\circ} \mathrm{C}, \mu_{\mathrm{w}}=0.35 \mathrm{cp}, \mu_{\mathrm{E}}=0.45\) cp. Other data are in Problem 10.E1.

Problem 10.E1

We are separating an ethanol-water mixture in a column operating at atmospheric pressure with a total condenser and a partial reboiler. Constant molal overflow (CMO) can be assumed, and reflux is a saturated liquid. Feed rate is \(100.0 \mathrm{lbmol} / \mathrm{h}\) of a \(30.0 \mathrm{~mol} \%\) ethanol mixture. The feed is a subcooled liquid, and 3.0 moles of feed will condense 1.0 mole of vapor at the feed plate. We desire \(\mathrm{x}_{\mathrm{D}}=0.8\) and \(\mathrm{x}_{\mathrm{B}}\) \(=0.01\), and use \(\mathrm{L} / \mathrm{D}=2.0\). Use a plate spacing of \(0.4572 \mathrm{~m}\). Downcomers occupy \(10 \%\) of the column cross-sectional area. Liquid densities are given in Perry's. The overall efficiency can be estimated from the O'Connell correlation. Note that the diameter calculated at different locations in the column will vary. Use the largest diameter calculated. Thus, you must either calculate a diameter at two or three locations in the column or justify why a given location will give the largest diameter.

a. What diameter is necessary if we will operate at \(75 \%\) of flooding? Use average values of physical parameters in stripping section and in enriching section.

b. How many real stages are required?

c. How tall is the column?

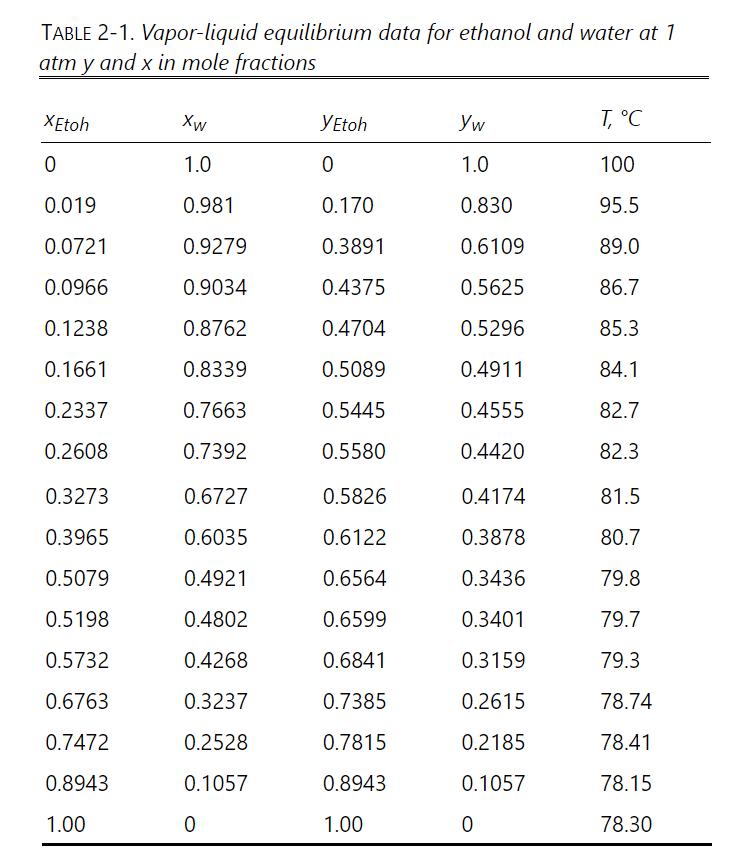
Data: Can estimate \(\mu\) from p. 99 Ethyl Alcohol Handbook at \(z=0.3=\) 0.523 wt.frac., \(\mu=0.55 \mathrm{cp}\). Distillate \(ho_{\mathrm{L}}=0.766 \mathrm{~g} / \mathrm{ml}\). \(\sigma\), surface tension in dyne \(/ \mathrm{cm}\). Handbook of Physics and Chemistry: Ethanol mole fraction \(\mathrm{x}_{\mathrm{E}}=0.01, \sigma \sim 46 \mathrm{dyn} / \mathrm{cm} ; \mathrm{x}_{\mathrm{E}}=0.3, \sigma \sim 25 \mathrm{dyn} / \mathrm{cm} ; \mathrm{x}_{\mathrm{E}}=0.8, \sigma\) \(\sim 18.6 \mathrm{dyn} / \mathrm{cm}\). The surface tension may be extrapolated as a linear function of temperature. VLE: Table 2-1. Vapor densities can be found from the perfect gas law.

Table 2-1

Transcribed Image Text:

TABLE 2-1. Vapor-liquid equilibrium data for ethanol and water at 1 atm y and x in mole fractions XEtoh Xw YEtoh Yw T, C 0 1.0 0 1.0 100 0.019 0.981 0.170 0.830 95.5 0.0721 0.9279 0.3891 0.6109 89.0 0.0966 0.9034 0.4375 0.5625 86.7 0.1238 0.8762 0.4704 0.5296 85.3 0.1661 0.8339 0.5089 0.4911 84.1 0.2337 0.7663 0.5445 0.4555 82.7 0.2608 0.7392 0.5580 0.4420 82.3 0.3273 0.6727 0.5826 0.4174 81.5 0.3965 0.6035 0.6122 0.3878 80.7 0.5079 0.4921 0.6564 0.3436 79.8 0.5198 0.4802 0.6599 0.3401 79.7 0.5732 0.4268 0.6841 0.3159 79.3 0.6763 0.3237 0.7385 0.2615 78.74 0.7472 0.2528 0.7815 0.2185 78.41 0.8943 0.1057 0.8943 0.1057 78.15 1.00 0 1.00 0 78.30