Repeat Problem 6.D4 except do the matrix and solution for the first trial for ethanol.

Problem 6.D4

A distillation column is separating \(100.0 \mathrm{kmol} / \mathrm{h}\) of a saturated liquid feed that is \(30.0 \mathrm{~mol} \%\) methanol, \(25.0 \mathrm{~mol} \%\) ethanol, \(35.0 \mathrm{~mol} \% \mathrm{n}-\) propanol, and \(10.0 \mathrm{~mol} \% \mathrm{n}\)-butanol at a pressure of \(1.0 \mathrm{~atm}\). The column has a total condenser and a partial reboiler. We want a \(98.6 \%\) recovery of n-propanol in the distillate and \(99.2 \%\) recovery of nbutanol in the bottoms (but realize that this first trial will not provide this amount of separation). Operation is with \(\mathrm{L} / \mathrm{D}=5, \mathrm{D}=60, \mathrm{~N}=4\), and \(\mathrm{N}_{\text {feed }}=3(\# 1=\) total condenser, and \#4 = partial reboiler). Set up the mass balance matrix Eq. (6-13) for the first trial for n-butanol and then solve. This is a hand calculation.

Equation 6-13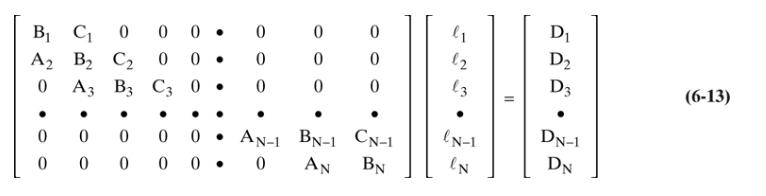

a. Use CMO to estimate liquid and vapor flow rates in the column for the first trial. Report these flow rates.

b. For a first guess of \(\mathrm{K}\) values, assume the \(\mathrm{K}\) values in the column are constant and equal to those found in a bubble-point calculation for the feed. The \(K_{n p}\) values are \((y / x)_{n p}\) where \(y_{n p}\) and \(x_{n p}\) are from the bubble-point calculation with constant alpha, Eq. (5-28) in Problem 5.C1. The other \(\mathrm{K}_{\mathrm{i}}=\alpha_{\mathrm{i}} \mathrm{K}_{\mathrm{np}}\).

Problem 5.C1.

c. Calculate all the A, B, C, and D values (but for n-butanol only), and write the complete matrix.

d. Solve the n-butanol matrix using the Thomas algorithm, and find the \(\mathrm{n}\)-butanol flow rates, \(\ell_{\mathrm{nC} 4, \mathrm{j}}\), leaving each stage.

e. The \(\mathrm{T}\) implicitly used in the calculation to find the \(\mathrm{K}\) values is the bubble-point temperature of the feed. To determine \(T\), first calculate the \(K\) value for \(n-\) propanol as \((y / x)_{n-\text { propanol }}\) where \(y\) and \(\mathrm{x}\) are found from the constant relative volatility solution for the bubble point. Then use Raoult's law to find the \(\mathrm{T}\) that gives this \(\mathrm{K}\) value. Report this temperature.
Do not do additional trials.
System properties: If we choose n-propanol as the reference, the relative volatilities are methanol \(=3.58\), ethanol \(=2.17\), \(n\)-propanol \(=\) 1.0 , and \(n\)-butanol \(=0.412\). These relative volatilities can be assumed to be constant. The \(\mathrm{K}\) value for \(\mathrm{n}\)-propanol can be estimated from Raoult's law. The vapor pressure data (in \(\mathrm{mm} \mathrm{Hg}\) ) for n-propanol from Perry's is:

Transcribed Image Text:

B C 0 00. 0 A2 B2 B2 C2 0 0. 0 0 A3 B3 B3 C3 0 0. 0 000 000 D1 12 D2 13. D3 (6-13) 00 00 0 00 AN-1 BN-1 CN-1 (N-1 DN-1 0 00. 0 AN BN IN DN