The topological optimization is discussed in chapter 1. Here, we will consider a topological optimization problem for a chemical process plant. The layout of the chemical process plant has been shown in Fig. 2.10. This plant consists of a water tank $(T)$, a pump $(P)$, a fan $(F)$, and a compressor $(C)$. The positions of the different units are also indicated in this figure in terms of their $(x, y)$ coordinates. It has been decided to add a new heat exchanger $(H)$ within this plant. Addition of new unit may cause congestion within the plant. It is decided to place $H$ within a rectangular area given by $\{-15 \leq x \leq 15,-10 \leq y \leq 10\}$ to avoid congestion. Formulate the optimization problem to find the position of $H$ to minimize the sum of its distances $x$ and $y$ from the existing units, $T, P, F$, and $C$.

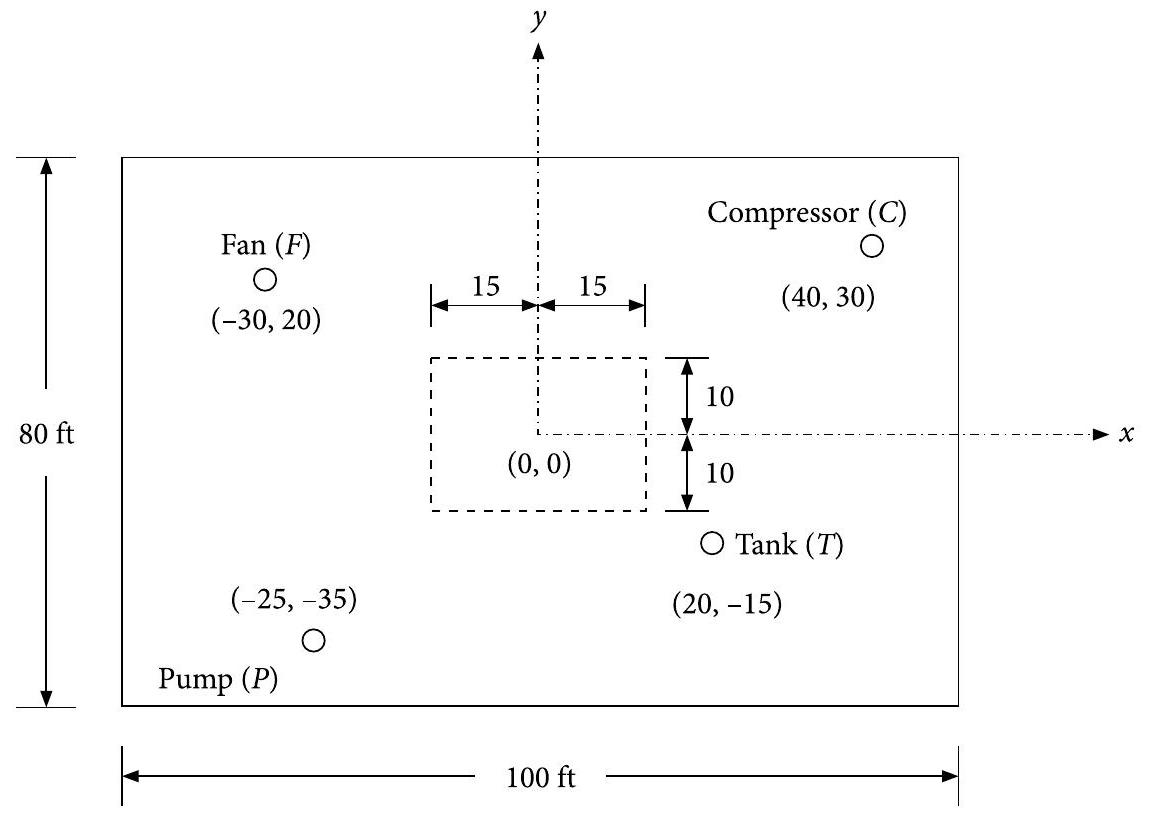
Fig. 2.10

Layout of a chemical processing plant (coordinates in $\mathrm{ft}$ )

80 ft Fan (F) 15 15 (-30, 20) (-25,-35) Pump (P) Compressor (C) (40, 30) 10 (0, 0) 10 100 ft Tank (T) (20, -15) x