The VLE data for formic acid (left(mathrm{CH}_{2} mathrm{O}_{2} ight))-water are presented in Table 8-6. a. Determine the

The VLE data for formic acid \(\left(\mathrm{CH}_{2} \mathrm{O}_{2}\right)\)-water are presented in Table 8-6.

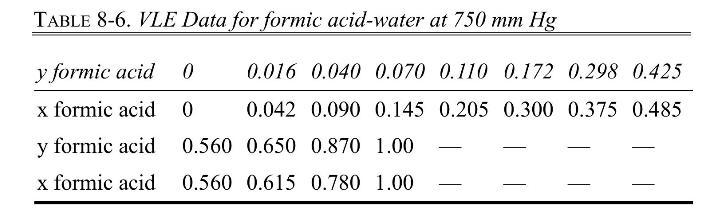
a. Determine the value of \(\alpha\) at each data point from \(\mathrm{x}_{\mathrm{A}}=0.042\) to \(\mathrm{x}_{\mathrm{A}}=\) 0.485 with Eq. (2-7a), and then calculate the geometric average value of \(\alpha\) using all data points. Use the geometric average value of \(\alpha\) in the Fenske equation to find \(\mathrm{N}_{\text {min }}\) at total reflux for a distillation column with a total condenser and a partial reboiler operating at \(750 \mathrm{~mm} \mathrm{Hg}\) if we want to have a distillate that is 0.015 mole fraction formic acid and a bottoms that is 0.54 mole fraction formic acid.

Equation (2-7a)

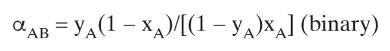
b. Plot Eq. (2-10a) with the geometric average value of \(\alpha\) from \(\mathrm{x}_{\mathrm{A}}=0\) to \(\mathrm{x}_{\mathrm{A}}=\mathrm{x}_{\mathrm{A}, \mathrm{az}}=0.560\left(\mathrm{~A}=\right.\) formic acid and \(\left.\mathrm{x}_{\mathrm{A}, \mathrm{az}}=0.560\right)\), and step off stages at total reflux.

Equation (2-10a)

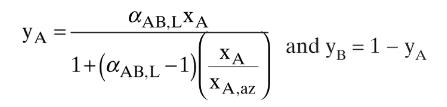
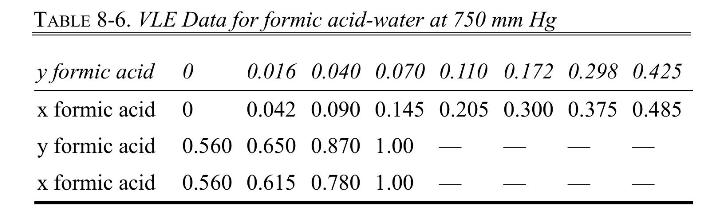
c. Plot the experimental equilibrium data from \(\mathrm{x}_{\mathrm{A}}=0\) to \(\mathrm{x}_{\mathrm{A}}=0.560\) on a McCabe-Thiele plot, draw a smooth curve through the data, and step off stages at total reflux.

d. Determine the linear equation for relative volatility, and use this equation to estimate the value of \(\mathrm{y}\) formic acid for the \(\mathrm{x}\) values from 0.042 to 0.485 in Table 8-6. Use the linearized equation for alpha to calculate an average relative volatility for the total reflux distillation problem in part \(\mathrm{a}\). Then calculate the value of \(\mathrm{N}_{\text {min }}\) with this \(\alpha_{\text {avg }}\).

e. Compare the results for the calculation of \(\mathrm{N}_{\text {min }}\) from parts \(\mathrm{a}, \mathrm{b}, \mathrm{c}\), and

d. Because \(\alpha\) is not constant, exact matches of part \(d\) with parts \

(a, b\), and \(\mathrm{c}\) are not expected.

At \(1.0 \mathrm{~atm}\) formic acid boils at \(100.8^{\circ} \mathrm{C}\). It forms a maximum boiling azeotrope with water that can be separated with a two-pressure distillation system. In the range of the distillation in this problem, formic acid is the less volatile component, which should not cause difficulties in use of the Fenske equation.

Transcribed Image Text:

TABLE 8-6. VLE Data for formic acid-water at 750 mm Hg y formic acid 0 0.016 0.040 0.070 0.110 0.172 0.298 0.425 x formic acid 0 y formic acid 0.042 0.090 0.145 0.205 0.300 0.375 0.485 0.560 0.650 0.870 1.00 x formic acid 0.560 0.615 0.780 1.00 -