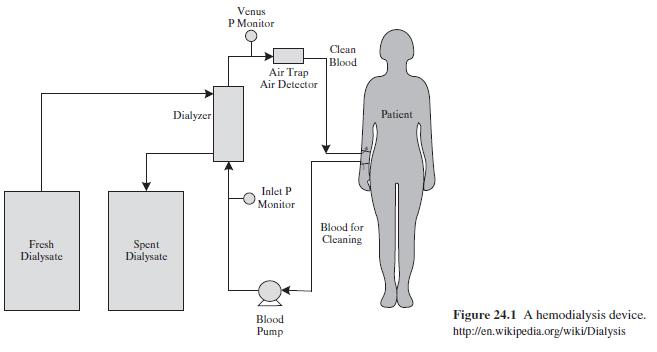
Consider the hemodialysis device using the hollow-fiber module in Figure 24.1, operating \(12 \mathrm{hr} / \mathrm{wk}\) (3 days, \(4 \mathrm{hr} /\) day) at a dialysis center. As shown in Example 24.1, with a blood flow rate of \(200 \mathrm{~mL} / \mathrm{min}\) and a dialysate flow rate of \(500 \mathrm{~mL} / \mathrm{min}\), its overall mass-transfer coefficient is estimated to be \(K_{i}=0.000468 \mathrm{~cm} / \mathrm{s}\).

(a) To design a home hemodialysis device, assume operation \(42 \mathrm{hr} / \mathrm{wk}(7\) days, \(6 \mathrm{hr} /\) day) while the patient sleeps. Reduce the blood flow rate by one-third (to \(133 \mathrm{~mL} / \mathrm{min}\) ) and the dialysate flow rate to \((300 \mathrm{~mL} / \mathrm{min})\) - a big advantage when sleeping. As a first step in redesigning the module, assume no changes in its geometry and estimate the mass-transfer coefficient inside the fiber, \(k_{b}\) (where the blood flows). Use the correlation:

\[N_{\mathrm{Sh}}=3.254\left[\frac{L / D_{i}}{N_{\mathrm{Pe}_{\mathrm{M}}}}\right]^{-1 / 3}\]

where \(L\) is the hollow-fiber length, \(D_{i}\) is its inside radius, \(N_{\mathrm{Sh}}\) is the Sherwood Number, and \(N_{\mathrm{Pe}_{\mathrm{M}}}\) is the Peclet Number for mass transfer. Then, assuming no change in the mass-transfer coefficient on the outside of the fibers, \(k_{d}\) (where the dialysate flows), estimate the reduction in \(K_{i}\).

(b) Increase the membrane permeability by a factor of 10 . Estimate the increase in \(K_{i}\).

Data From Example 24.1:-

Figure 24.1:-

Transcribed Image Text:

Develop a design procedure for a hollow-fiber hemodialysis device of the type shown in Figure 24.1. Base the design on a blood flow rate of 200 mL/min and a dialysate flow rate of 500 mL/min. Assume that the design will be controlled by mass transfer of one of the blood plasma components to be removed, for example, urea. The blood will flow through the hollow fibers, and the dialysate will flow past the outside surface of the fibers in a direction countercurrent to the flow of the blood plasma. A typical patient will require hemodialysis when the blood reaches a urea nitrogen level (BUN) of 100 mg/dL. A target for the hemodialysis device is to reduce the BUN to 30 mg/dL within 4 hr, which corresponds to normal operation at a hemodialysis center.