Given the basis sets of groups Set- (1left{mathrm{CH}_{3} ; mathrm{CH}_{2} ; mathrm{CH} ; mathrm{C} ight} ;) Set- (2left{mathrm{OH} ; mathrm{CH}_{3} mathrm{CO} ; mathrm{CH}_{3} mathrm{O} ;

Given the basis sets of groups Set- \(1\left\{\mathrm{CH}_{3} ; \mathrm{CH}_{2} ; \mathrm{CH} ; \mathrm{C}\right\} ;\) Set- \(2\left\{\mathrm{OH} ; \mathrm{CH}_{3} \mathrm{CO} ; \mathrm{CH}_{3} \mathrm{O} ; \mathrm{CH}_{2} \mathrm{CO}, \mathrm{CH}_{2} \mathrm{O}\right\}\), how many chemically feasible molecules can be generated [satisfying Eqs. (4.1)-(4.5)] with a minimum of two groups and a maximum of four groups and any number of groups from Set-1, but a maximum of one group from Set-2? If there were no restrictions, how many structures could be generated?

Data From Eqs. 4.1 - 4.5:-

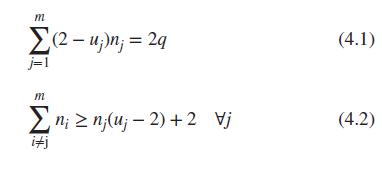
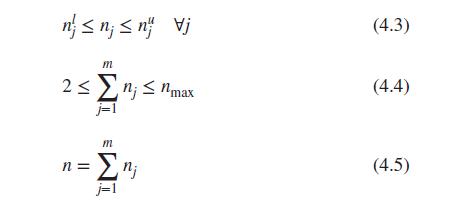
m (2-u;)n; = 29 j=1 m n; nju; -2)+2 vj i#j (4.1) (4.2)