a. Example 15-1: Finding the Effective Diffusivity of De Wolfram 1. Can you think up a question
Question:
a. Example 15-1: Finding the Effective Diffusivity of De
Wolfram
1. Can you think up a question about the sliders that would be somewhat interesting? I am not sure I can, that’s why there is no specific question here.
Example 15-1
Using typical values of DAB, ϕp, σc, and τ, estimate the effective diffusivity, De.
b. Example 15-3: Reducing Nitrous Oxides in a Plant’s Effluent. This is a Stop and Smell the Roses Simulation.
Wolfram
1. Which parameter has the larger impact in reducing internal diffusion limitations, pellet radius or internal surface area?
2. Vary and list at least three parameters which can be changed to achieve approximately 90% conversion for a new flow rate of 10–5 m3/s.
3. Which combination of parameter values causes the surface reaction rate to become the closest to the internal diffusion rate, that is, WP ~ 1?
4. For the base case, calculate the percent of the total resistance for each of the individual resistances of external diffusion, internal diffusion, and surface reaction.
5. Qualitatively, how would each of your percentages change if the temperature were increased significantly?
6. Vary various parameters to see the effect of each parameter on Mears number, MR and write a set of conclusions.
7. What variable affects the internal effectiveness factor the most?
8. What variable affects the overall effectiveness factor the most?
9. What variable affects the Mears criteria (MR) the most?
10. What variable affects the Weisz–Prater (WP) the most?
11. Apply the Weisz–Prater criteria to a particle 0.005 m in diameter.
12. Write a set of conclusions for your experiments (i) through (xi).
Polymath
1. How would your answers in (i) through (v) change if the reaction were zero order with k0 = 9 × 10–4 mol/g/s. Hint: What are the new equations for η and Ω?
2. Overall Effectiveness Factor. Calculate the percent of the total resistance for the resistance of external diffusion, internal diffusion, and surface reaction. Qualitatively, how would each of your percentages change?
3. What if you applied the Mears and Weisz–Prater criteria to Examples 15-4 and 15-3? What would you find? What would you learn if ΔHRx∘ = –25 kcal/mol, h = 100 Btu/h • ft2 • °F, and E = 20 kcal/mol?
4. What if your internal surface area decreased with time because of sintering. Describe how your effectiveness factor would change and
the rate of reaction change with time if kd = 0.01 h–1 and η = 0.01 at t = 0? Explain, being as quantitative as possible when you can.
5. What if you were to assume that the resistance to gas absorption in the CRE Web site Professional Reference Shelf R15.1 was the same as in Professional Reference Shelf R15.3 and that the liquid-phase reactor volume in Professional Reference Shelf R15.3 was 50% of the total? Could you determine the limiting resistance? If so, what is it? What other things could you calculate in Professional Reference Shelf R15.1 (e.g., selectivity, conversion, molar flow rates in and out)? Hint: Some of the other reactions that occur include
CO+3H2→CH4+H2OH2O+CO→CO2+H2
Example 15-3
This is a Stop and Smell the Roses Example. Exploring this LEP Example with Wolfram and/or Python that will give you a fantastic intuitive feel of the parameters and conditions that result in internal and external diffusion limitations. We have seen that Nitric Oxide (NO) plays an important role in smog formation and there are great incentives for reducing its concentration in the atmosphere. It is proposed to reduce the concentration of NO in an effluent stream from a plant by passing it through a packed bed of spherical, porous carbonaceous solid pellets. A 2% NO and 98% air mixture flows at a rate of 1 × 10–6 m3/s (0.001 dm3/s) through a 2-in.-ID tube packed with porous solid pellets at a temperature of 1173 K and a pressure of 101.3 kPa. The reaction
NO + C→CO+12 N2
Green chemical reaction engineering is pseudo first order in NO because of the excess of carbon surface area; that is,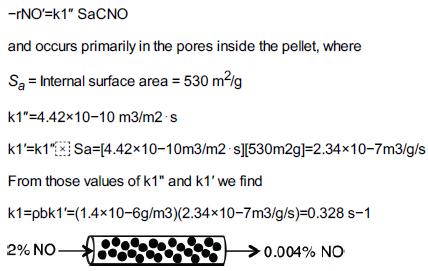
1. Derive an equation to find the conversion profiles, X = f(W).
2. Calculate the Thiele modulus ϕ1 and the η internal effectiveness factor.
3. Calculate the Weisz–Prater parameter, WP. Is internal mass transfer limiting?
4. Calculate the overall effectiveness factor, Ω
5. Calculate the Mears parameter, MR. Is external mass transfer limiting?
6. Calculate the weight of solid porous catalyst necessary to reduce the NO concentration of 0.004%, which is below the Environmental Protection Agency’s limit.
A spherical cell or circle represents the Porous catalyst pellet. The reactant with concentration C subscript Ab undergoes external resistance and enters through the pore of the catalyst pellet. The concentration now is C subscript As. Further, the reactant undergoes internal resistance and the concentration is C subscript A.
Additional information:
Step by Step Answer:
