The production of a product P from a particular gram-negative bacteria follows the Monod growth law rg=maxCsCcKS+Cs

The production of a product P from a particular gram-negative bacteria follows the Monod growth law
rg=μmaxCsCcKS+Cs
with μmax = 1 h^–1, K_S = 0.25 g/dm³, and Y_c/s = 0.5 g/g.
a. The reaction is to be carried out in a batch reactor with the initial cell concentration of C_c0 = 0.1 g/dm³ and substrate concentration of C_s0 = 20 g/dm³.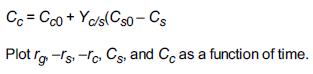

b. The reaction is now to be carried out in a CSTR with C_s0 = 20 g/dm³ and C_c0 = 0. What is the dilution rate at which washout occurs?
c. For the conditions in part (b), what is the dilution rate that will give the maximum product rate (g/h) if Yp/c = 0.15 g/g? What are the concentrations Cc, Cs, Cp, and
–rs at this value of D?
d. How would your answers to (b) and (c) change if cell death could not be neglected with kd = 0.02 h^–1?
e. How would your answers to (b) and (c) change if maintenance could not be neglected with m = 0.2 g/h/dm³?

f. Redo part (a) and use a logistic growth law
rg=μmax(1−CcC∞)Cc
and plot C_c and r_c as a function of time. The term C_∞ is the maximum cell mass concentration and is called the carrying capacity, and is equal to C_∞ = 1.0 g/dm³. Can you find an analytical solution for the batch reactor? Compare with part (a) for C_∞ = Y_c/s C_s0 + C_c0.

Transcribed Image Text:

Cc Cco + Yc/s(Cso-Cs Plot rg-rs-ro Cs, and Co as a function of time.