A heat pump used to warm a home must employ a cycle that produces a working fluid
Question:
A heat pump used to warm a home must employ a cycle that produces a working fluid at temperatures greater than typical indoor temperature so that heat transfer to the inside can take place. Similarly, it must produce a working fluid at temperatures that are colder than the outdoor temperature so that heat transfer occurs from outside. Its hot and cold reservoir temperatures therefore cannot be too close, placing a limit on its COPhp. (See Figure 15.29.) What is the best coefficient of performance possible for such a heat pump, if it has a hot reservoir temperature of 45.0°C and a cold reservoir temperature of -15.0°C?
Strategy
A Carnot engine reversed will give the best possible performance as a heat pump. As noted above, COPhp = 1/Eff, so that we need to first calculate the Carnot efficiency to solve this problem.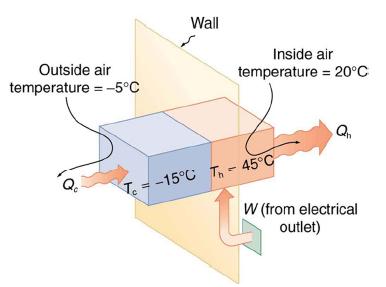
Step by Step Answer:






