Given that the Moon orbits Earth each 27.3 d and that it is an average distance of
Question:
Given that the Moon orbits Earth each 27.3 d and that it is an average distance of 3.84 x 108 m from the center of Earth, calculate the period of an artificial satellite orbiting at an average altitude of 1500 km above Earth's surface.
Strategy
The period, or time for one orbit, is related to the radius of the orbit by Kepler’s third law, given in mathematical form in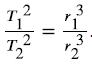
Let us use the subscript 1 for the Moon and the subscript 2 for the satellite. We are asked to find T2. The given information tells us that the orbital radius of the Moon is r1 = 3.84 x 108 m, and that the period of the Moon is T1 = 27.3 d. The height of the artificial satellite above Earth's surface is given, and so we must add the radius of Earth (6380 km) to get r2 =(1500+ 6380) km = 7880 km. Now all quantities are known, and so T2 can be found.
Step by Step Answer:
Keplers third law is To solve for T 2 we crossmultiply and take the square roo...View the full answer
