In the collision pictured in Figure 8.9, two carts collide inelastically. Cart 1 (denoted m carries a spring which is initially compressed. During the collision, the spring releases its potential energy and converts it to internal kinetic energy. The mass of cart 1 and the spring is 0.350 kg, and the cart and the spring together have an initial velocity of 2.00 m/s. Cart 2 (denoted m₂ in Figure 8.9) has a mass of 0.500 kg and an initial velocity of -0.500 m/s. After the collision, cart 1 is observed to recoil with a velocity of -4.00 m/s.

(a) What is the final velocity of cart 2? 

(b) How much energy was released by the spring (assuming all of it was converted into internal kinetic energy)?

Data given in Figure 8.9

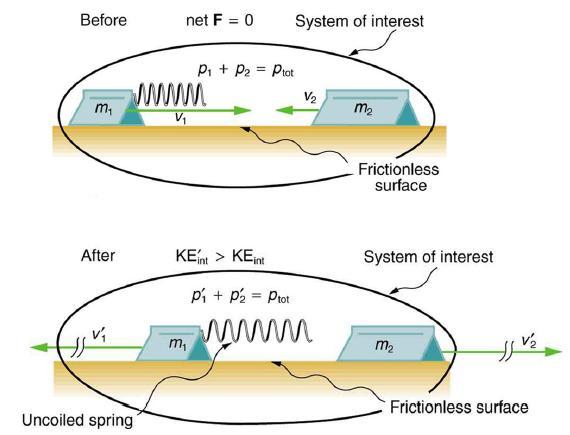
Strategy

We can use conservation of momentum to find the final velocity of cart 2, because F_net=0 (the track is frictionless and the force of the spring is internal). Once this velocity is determined, we can compare the internal kinetic energy before and after the collision to see how much energy was released by the spring.

Transcribed Image Text:

Before m₁ After أنا را Uncoiled spring net F = 0 V₁ P₁ + P₂ = Ptot KEint > KE int m₁ P₁ + P₂ = Prot System of interest V₂ m₂ Frictionless surface System of interest m₂ V/₂ Frictionless surface