A 30-g bullet with a speed of 400 m/s strikes a glancing blow to a target brick of mass 1.0 kg. The brick breaks into two fragments. The bullet deflects at an angle of 30° above the +x-axis and has a reduced speed of 100 m/s. One piece of the brick (with mass 0.75 kg) goes off to the right, or in the initial direction of the bullet, with a speed of 5.0 m/s. (a) Taking the +x-axis to the right, will the other piece of the brick move in the (1) second quadrant, (2) third quadrant, or (3) fourth quadrant? (b) Determine the speed and direction of the other piece of the brick immediately after collision (where gravity can be neglected).

(a) The conservation of linear momentum can be applied because there is no net external force on the system – the bullet and brick. Initially, all of the momentum is in the forward +x-direction (Figure 6.10). Afterward, one piece of the bricflies off in the +x-direction, and the bullet at an angle of 30° to the x-axis. The bullet’s momentum has a positive y-component, so the other piece of the brick must have a negative y-component because there was no initial momentum in the y-direction. Hence, with the total momentum in the +x-direction (before and after), the answer is (3) fourth quadrant.

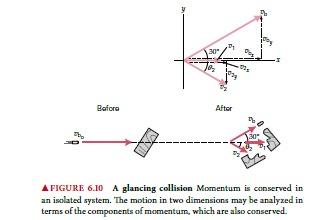(b) There is one object with momentum before collision (the bullet), and three with momenta afterward (the bullet and the two fragments). By the conservation of linear momentum, the total (vector) momentum after collision equals that before collision. As is often the case, a sketch of the situation is helpful, with the vectors resolved in component form (Figure 6.10). Applying the conservation of linear momentum should allow the velocity (speed and direction) of the second fragment to be determined.  

Transcribed Image Text:

30 Before After 30 FIGURE 6.10 A glancing collision Momentum is conserved in an isolated system. The motion in two dimensions may be analyzed in terms of the components of momentum, which are also conserved.