Real-life situations are generally complicated, but some can be approximately analyzed by using simple models. Such a model for a skater's spin is shown in \(\square\) Figure 8.26, with a cylinder and rods representing the skater. In (a), the skater goes into the spin with the "arms" out, and in (b) the "arms" are over the head to achieve a faster spin by the conservation of angular momentum. If the initial spin rate is 1 revolution per \(1.5 \mathrm{~s}\), what is the angular speed when the arms are tucked in?

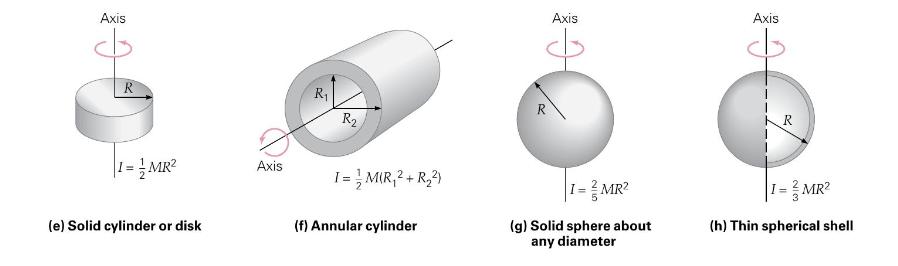
THINKING IT THROUGH. The body and arms of a skater are approximated by the cylinder and rods, for which the moments of inertia are known (Figure 8.17). Special attention must be given to finding the moment of inertia of the arms around the axis of rotation (through the cylinder). This can be done by applying the parallel axis theorem (Equation 8.8).

With the angular momentum conserved, \(L=L_{\mathrm{o}}\) or \(I \omega=I_{\mathrm{o}} \omega_{\mathrm{o}}\). Knowing the initial angular speed, and given quantities to evaluate the moments of inertia (Figure 8.26), the final angular speed can be found.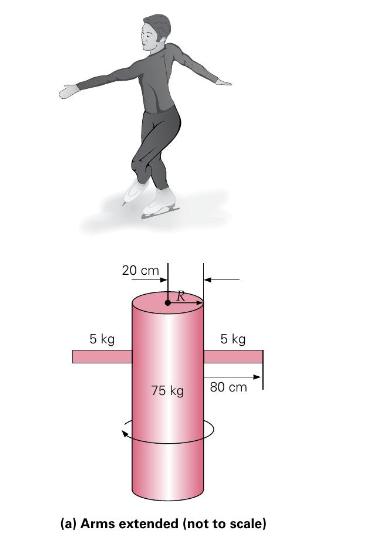

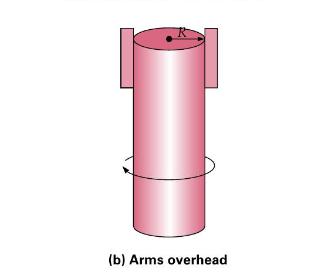
Figure (8.17):

Transcribed Image Text:

5 kg 20 cm 5 kg 75 kg 80 cm (a) Arms extended (not to scale)