Suppose the LED band gap is \(2.5 \mathrm{eV}\), which corresponds to a wavelength of \(500 \mathrm{~nm}\). Consider the possible electron transitions in Figure P29.76. \(500 \mathrm{~nm}\) is the

A. Maximum wavelength of the LED.

B. Average wavelength of the LED.

C. Minimum wavelength of the LED.

Light-emitting diodes, known by the acronym LED, produce the familiar green and red indicator lights used in a wide variety of consumer electronics. LEDs are semiconductor devices in which the electrons can exist only in certain energy levels. Much like molecules, the energy levels are packed together close enough to form what appears to be a continuous band of possible energies. Energy supplied to an LED in a circuit excites electrons from a valence band into a conduction band. An electron can emit a photon by undergoing a quantum jump from a state in the conduction band into an empty state in the valence band, as shown in Figure P29.76.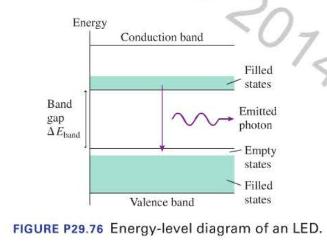

The size of the band gap \(\Delta E_{\text {band }}\) determines the possible energies — and thus the wavelengths-of the emitted photons. Most LEDs emit a narrow range of wavelengths and thus have a distinct color.
This makes them well-suited for traffic lights and other applications where a certain color is desired, but it makes them less desirable for general illumination. One way to make a "white" LED is to combine a blue LED with a substance that fluoresces yellow when illuminated with the blue light. The combination of the two colors makes light that appears reasonably white.

Transcribed Image Text:

2014 Energy Conduction band Filled Band gap AEtand states Emitted photon Empty states Filled states Valence band FIGURE P29.76 Energy-level diagram of an LED.