In addition to tanh, another s-shaped smooth function, the logistic sigmoid function y=1 / (1+exp(–x)),

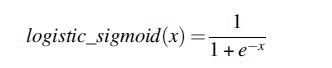
is commonly used as an activation function in neural networks. A common way to implement them in fixed-point arithmetic uses a piecewise quadratic approximation, where the most significant bits of the input value select which table entry to use. Then the least significant bits of the input value are sent to a degree-2 polynomial that describes a parabola that is fit to the subrange of the approximated function.

a. Using a graphing tool (we like www.desmos.com/calculator), draw the graphs for the logistic sigmoid and tanh functions.

b. Now draw the graph of y=tanh (x/2)/2. Compare that graph with the logistic sigmoid function. How much do they differ by? Build an equation that shows how to transform one into the other. Prove that your equation is correct.

c. Given this algebraic identity, do you need to use two different sets of coefficients to approximate logistic sigmoid and tanh?

d. Tanh is an odd function, meaning that f(-x) = -f(x). Can you exploit this fact to save table space?

e. Let's focus our attention on approximating tanh over the interval x = [0.0, 6.4] on the number line. Using floating-point arithmetic, write a pro- gram that divides the interval into 64 subintervals (each of length 0.1), and then approximates the value of tanh over each subinterval using a single constant floating-point value (so you'll need to pick 64 different floating-point values, one for each subinterval). If you spot-check 100 different values (randomly chosen is fine) within each subinterval, what is the worst-case approximation error you see over all subintervals? Can you choose your constant to minimize the approximation error for each subinterval?

f. Now consider building a floating-point linear approximation for each sub- interval. In this case, you want to pick a pair of floating-point values m and b, for the traditional line equation y=mx + b, to approximate each of the 64 subintervals. Come up with a strategy that you think is reasonable to build this linear interpolation over 64 subintervals for tanh. Measure the worst-case approximation error over the 64 intervals. Is your approximation monotonic when it reaches a boundary between subintervals?

g. Next, build a quadratic approximation, using the standard formula y = ax +bx+c. Experiment with a number of different ways to fit the formula. Try fitting the parabola to the endpoints and midpoint of the bucket, or using a Taylor approximation around a single point in the bucket. What worst-case error do you get?

h. (extra credit) Let's combine the numerical approximations of this exercise with the fixed-point arithmetic of the previous exercise. Suppose that the input x = [0.0, 6.4] is represented by a 15-bit unsigned value, with Ox0000 represent- ing 0.0 and 0x7FFF representing 6.4. For the output, similarly use a 15-bit unsigned value, with 0x0000 representing 0.0 and 0x7FFF representing 1.0. For each of your constant, linear, and quadratic approximations, calculate the combined effect of approximation and quantization errors. Since there are so few input values, you can write a program to check them exhaustively.

i. For the quadratic, quantized approximation, is your approximation mono- tonic within each subinterval?

j. A difference of one ulp in the output scale should correspond to an error of 1.0/32767. How many ulps of error are you seeing in each case?

k. By choosing to approximate the interval [0.0, 6.4], we effectively clipped the "tail" of the hyperbolic tangent function, for values of x>6.4. It's not an unreasonable approximation to set the output value for all of the tail to 1.0. What's the worst-case error, in terms of both real numbers and ulps, of treating the tail this way? Is there a better place we might have clipped the tail to improve our accuracy?

Transcribed Image Text:

logistic_sigmoid(x) = 1 1 + ex