In Program 4.1, the “view” matrix is defined in the display() function simply as the negative of the camera location:

Replace this code with an implementation of the computation shown in Figure 3.13. This will allow you to position the camera by specifying a camera position and three orientation axes. You will find it necessary to store the vectors U,V,N described in Section 3.7. Then, experiment with different camera viewpoints, and observe the resulting appearance of the rendered cube.

Program 4.1

Figure 3.13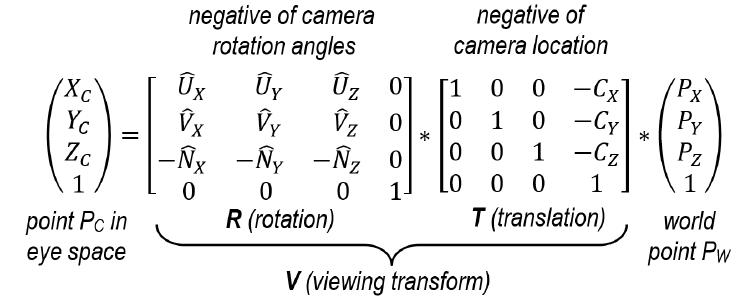

Section 3.7

So far, the transform matrices we have seen all operate in 3D space. Ultimately, however, we will want to display our 3D space—or a portion of it—on a 2D monitor. In order to do this, we need to decide on a vantage point. Just as we see our real world through our eyes from a particular point, in a particular direction, so too must we establish a position and orientation as the window into our virtual world. This vantage point is called “view” or “eye” space, or the “synthetic camera.”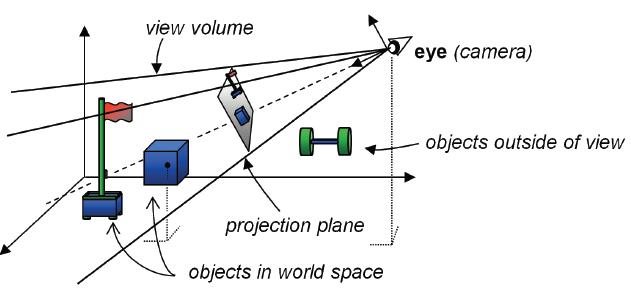

vMat.translation(-cameraX, -cameraY, -cameraZ);