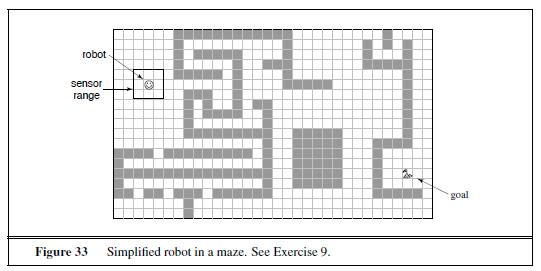
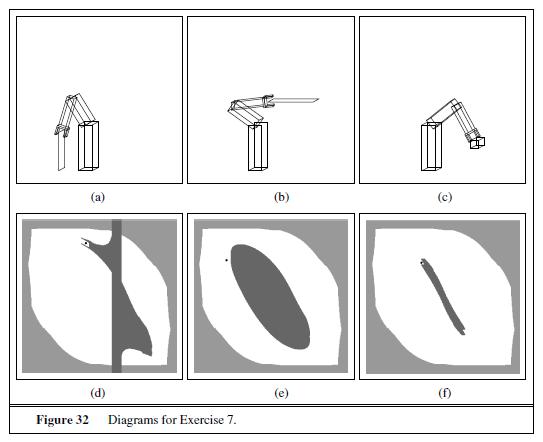
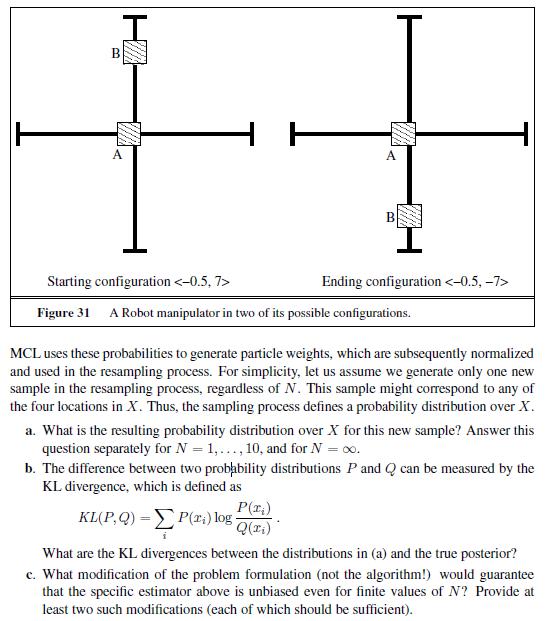
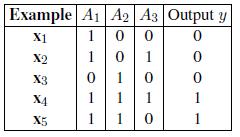
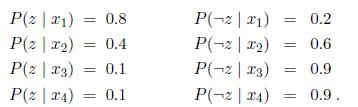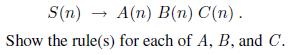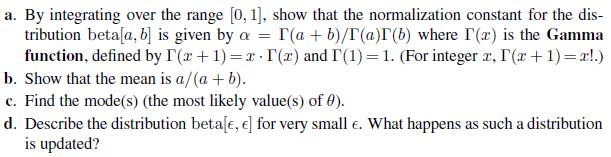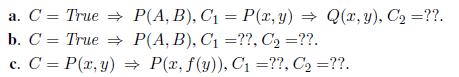Artificial Intelligence A Modern Approach 3rd Edition Stuart Russell - Solutions
Discover the ultimate resource for mastering "Artificial Intelligence: A Modern Approach 3rd Edition" by Stuart Russell. Access comprehensive solutions, including a complete answers key and step-by-step answers for every chapter. Our online platform offers a detailed solution manual and solved problems, perfect for enhancing your understanding. Download the solutions PDF for free and explore the extensive test bank designed to challenge and improve your knowledge. Ideal for students and instructors alike, our instructor manual and textbook resources provide invaluable support for academic success. With free downloads and insightful chapter solutions, excel in your AI studies today!
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()