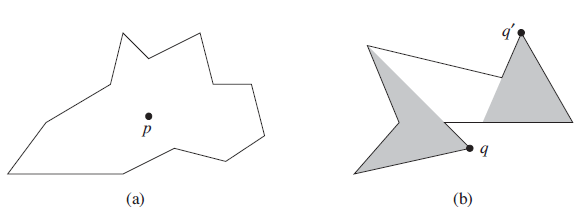
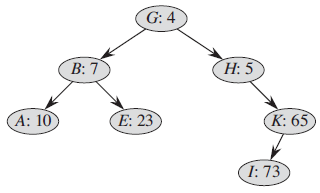
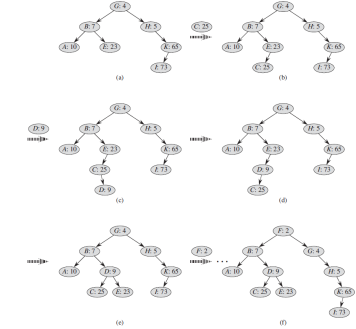
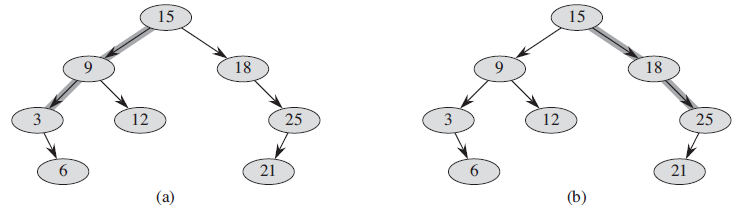
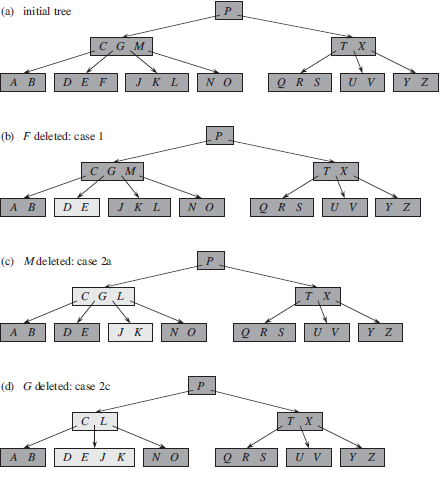
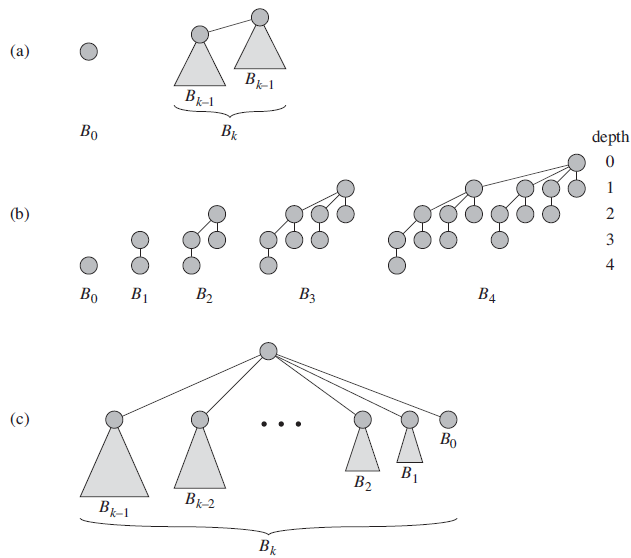
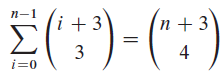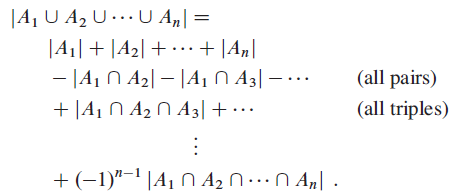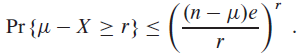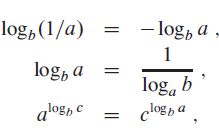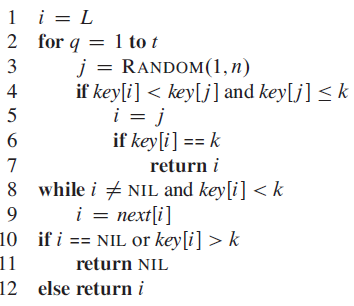Data Structures and Algorithms in Java 6th edition Michael T. Goodrich, Roberto Tamassia, Michael H. Goldwasser - Solutions
Explore the comprehensive world of "Data Structures and Algorithms in Java, 6th Edition" with our exclusive online solutions. Dive into expertly crafted answers key and solution manual, providing precise guidance for every problem. Our solutions pdf offers solved problems with detailed questions and answers tailored for each chapter. Whether you're seeking a test bank or instructor manual, our resources ensure step-by-step answers to enhance your understanding. This textbook's chapter solutions are now accessible for free download, empowering your learning journey with clarity and precision. Unlock the full potential of your studies with our unparalleled support.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()