Consider the system I and system II shown below. The system I can be reduced to the form as shown in system II with

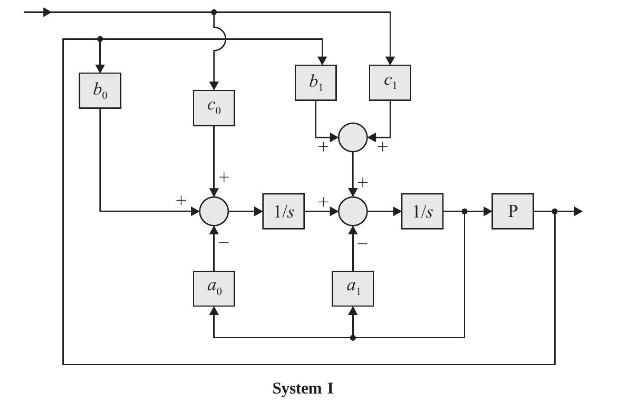
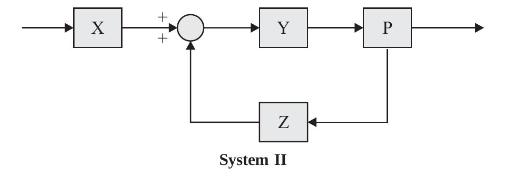
(a) \(\mathrm{X}=c_{0} s+c_{1}\), Y \(=\frac{1}{s^{2}+a_{0} s+a_{1}}, \mathrm{Z}=b_{0} s+b_{1}\)
(b) \(\mathrm{X}=1\), Y \(=\frac{c_{0} s+c_{1}}{s^{2}+a_{0} s+a_{1}}, \mathrm{Z}=b_{0} s+b_{1}\)
(c) \(\mathrm{X}=c_{1} s+c_{0}, \mathrm{Y}=\frac{b_{1} s+b_{0}}{s^{2}+a_{0} s+a_{1}}, \mathrm{Z}=1\)
(d) \(\mathrm{X}=c_{1} s+c_{0}, \mathrm{Y}=\frac{1}{s^{2}+a_{0} s+a_{1}}, \mathrm{Z}=b_{1} s+b_{0}\)

Transcribed Image Text:

bo Co ao 44 b C 1/s + System I a + 1/s P