A linear model of the -subsystem of a grid-connected voltage-source converter with a Y-Y transformer (Mahmood, 2012)
Question:
A linear model of the α-subsystem of a grid-connected voltage-source converter with a Y-Y transformer (Mahmood, 2012) was presented in Problem 69, Chapter 8, and Problem 51, Chapter 10. The system was represented with unity-feedback and a forward path consisting of the cascading of a compensator and a plant. The plant is given by
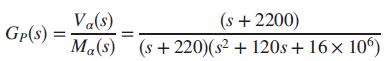
This system is now to be digitally controlled with the following specifications: percent overshoot, %OS = 10%; settling time, TS = 0.1 second; and sampling interval, T = 0.001 second. Design a lead compensator for that system to meet these specifications.
Data From Problem 69 Chapter 8:
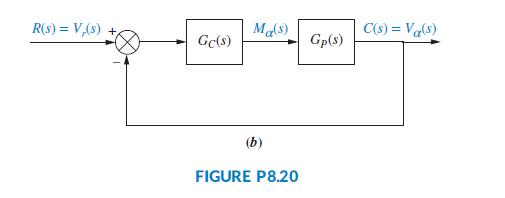
A linear dynamic model of the α-subsystem of a grid connected voltage-source converter (VSC) using a Y-Y transformer is showninFigureP8.20(a) (Mahmood, 2012). Here, C = 135μF; R1 = 0.016Ω; L1 = 0.14mH; R2 = 0.014Ω; L2 = 10 μH; Rg = 1.1Ω; and Lg = 0.5mH.
a. Find the transfer function GP(s) = Vα(s)/Mα(s0.
b. If GP(s) is the plant in Figure P8.20(b) and GC(s) = K, use MATLAB to plot the root locus. On a closeup of the locus (from 300 to 0 on the real axis and from 50 to 5000 on the imaginary axis), find K and the coordinates of the dominant poles, which correspond to ζ = 0.012. Plot
the output response, c(t) = vα(t), at that value of the gain when a step input, r(t)= vr (t)= 208 u(t) volts, is applied at t = 0. Mark on the time response graph, c(t), all relevant characteristics, such as the percent overshoot, peak time, rise time, settling time, and final steady-state value.
Data From Problem 51 Chapter 10:
A linear model of the α-subsystem of a grid connected voltage-source converter (VSC) with a Y-Y transformer (Mahmood, 2012) was presented in Problem 69, Chapter 8. In Figure P8.20(b), GC(s) = K and GP(s) is given in a pole zero form (with a unity gain and slightly modified parameters) as follows:
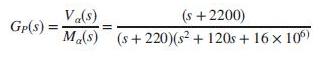
Step by Step Answer:





