For Problem 23 in Chapter 1 we developed the functional block diagrams for the cruise control of serial, parallel, and split-power

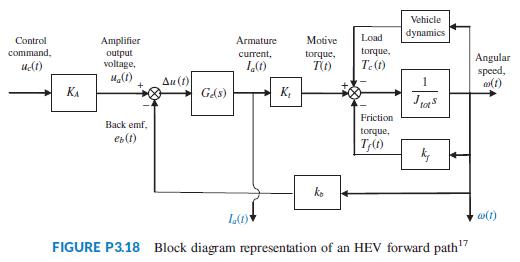
hybrid electric vehicles (HEV). Those diagrams showed that the engine or electric motor or both may propel the vehicle. When electric motors are the sole providers of the motive force, the forward paths of all HEV topologies are similar. In general, such a forward path can be represented (Preitl, 2007) by a block diagram similar to the one of Figure P3.18. Assume the motor to be an armature-controlled dc motor. In this diagram, K_A is the power amplifier gain; G_e(s) is the transfer function of the motor electric circuit and consists of a series inductor and resistor, L_a and R_a, respectively; K_t is the motor torque constant; J_tot, is the sum of the motor inertia, J_m, the inertias of the vehicle, J_veh, and the two driven wheels, J_w, both of which are reflected to the motor shaft; k_f is the coefficient of viscous friction; and kb is the back e_mf constant. The input variables are u_c(t), the command voltage from the electronic control unit and T_c(t), the load torque. The output variables in this block diagram are the motor angular speed, ω(t), and its armature current, I_a(t).

a. Write the basic time-domain equations that characterize the relationships between the state, input, and output variables for the block diagram of Figure P3.18, given that the state variables are the motor armature current, Ia(t), and angular speed, ω(t).

b. Write the resulting state-space equations and then represent them in matrix form. Regard the load torque T_c(t) as an extra input to the system. Thus, in your resulting state-space representation, the system will have two inputs and two outputs.

Data From Problem 23:

A linear, time-invariant model of the hypothalamic pituitary-adrenal axis of the endocrine system with five state variables has been proposed as follows (Kyrylov, 2005):

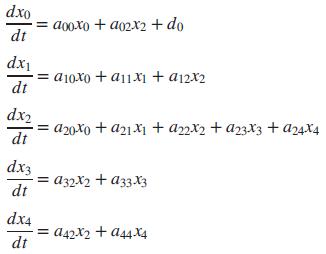
where each of the state variables represents circulatory concentrations as follows:

x₀ = corticotropin-releasing hormone

x₁ = corticotropin

x₂ = free cortisol

x₃ = albumin-bound cortisol

x₄ = corticosteroid-binding globulin

d₀ = an external generating factor

Express the system in the form ẋ = Ax + Bu.

Vehicle dynamics Control Amplifier Armature Motive Load ommand, torque, output voltage, current, torque, T(t) Angular speed, T.(1) Au (1) KA GAs) K, Friction Back emf, torque, eb(t) ko w(1) FIGURE P3.18 Block diagram representation of an HEV forward path"