It has been shown (Pounds, 2011) that an unloaded UAV helicopter is closed-loop stable and will have a characteristic equation given by

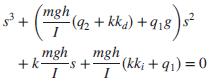
where m is the mass of the helicopter, g is the gravitational constant, I is the rotational inertia of the helicopter, h is the height of the rotor plane above the center of gravity, q₁ and q₂ are stabilizer flapping parameters, k, k_i, and k_d are controller parameters; all constants > 0. The UAV is supposed to pick up a payload; when this occurs, the mass, height, and inertia change to m´, h´, and I´, respectively, all still > 0. Show that the helicopter will remain stable as long as

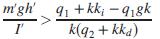
mgh (42 + kka) +918 mgh (kk; + 91) = 0 I mgh +k- I