Question: It was shown in Chapter 6, Problem 68, that when the virus levels in an HIV/ AIDS patient are controlled using RTIs the linearized plant
It was shown in Chapter 6, Problem 68, that when the virus levels in an HIV/ AIDS patient are controlled using RTIs the linearized plant model is
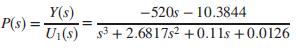
Assume that the system is embedded in a configuration, such as the one shown in Figure P9.1, where G(s) = Gc(s) P(s). Here, Gc(s) is a cascade compensator. For simplicity in this problem, choose the dc gain of Gc(s) less than zero to obtain a negative feedback system (the negative signs of Gc(s) and P(s) cancel out) (Craig, I. K., 2004).
a. Consider the uncompensated system with Gc(s) = -K. Find the value of K that will place all closed-loop poles on the real axis.
b. Use MATLAB to simulate the unit-step response of the gain compensated system. Note the %OS and the Ts from the simulation.
c. Design a PI compensator so that the steady-state error for step inputs is zero. Choose a gain value to make all poles real.
d. Use MATLAB to simulate the design in Part c for a unit step input. Compare the simulation to Part b.
Data from Chapter 6, Problem 68:
The HIV infection linearized model developed in Problem 84,Chapter 4, can be shown to have the transfer function
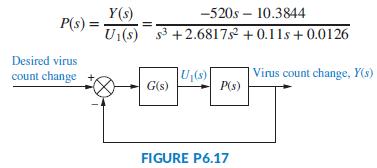
It is desired to develop a policy for drug delivery to maintain the virus count at prescribed levels. For the purpose of obtaining an appropriate u1(t); feedback will be used as shown in Figure P6.17 (Craig, 2004). As a first approach, consider G(s) = K; a constant to be selected. Use the Routh-Hurwitz criteria to find the range of K for which the system is closed-loop stable.
Data from Problem 84,Chapter 4:
We developed a linearized state-space model of HIV infection. The model assumed that two different drugs were used to combat the spread of the HIV virus. Since this book focuses on single-input, single output systems, only one of the two drugs will be considered. We will assume that only RTIs are used as an input. Thus, in the equations of Chapter 3, Problem 31, u2 = 0 (Craig, 2004).
a. Show that when using only RTIs in the linearized system of Problem 31, Chapter 3, and substituting the typical parameter values given in the table of Problem 31c, Chapter 3, the resulting state-space representation for the system is given by
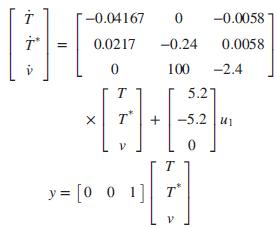
b. Obtain the transfer function from RTI efficiency to virus count; namely, find Y(s)/U1(s).
c. Assuming RTIs are 100% effective, what will be the steady-state change of virus count in a given infected patient? Express your answer in virus copies per ml of plasma. Approximately how much time will the medicine take to reach its maximum possible effectiveness?
Data from Chapter 3, Problem 31:
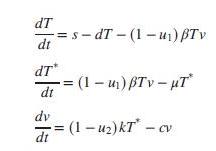
Y(s) -520s 10.3844 P(s)= U1(s) s3 + 2.6817s2 +0.1 1s +0.0126
Step by Step Solution
3.52 Rating (165 Votes )
There are 3 Steps involved in it
There wa... View full answer

Get step-by-step solutions from verified subject matter experts


