Problem 47, Chapter 8 discusses a magnetic levitation system with a plant transfer function P(s) = 1300/s 2 - 860 2 (Galvo, 2003). Assume that

Problem 47, Chapter 8 discusses a magnetic levitation system with a plant transfer function P(s) =  1300/s² - 860² (Galvão, 2003). Assume that the plant is in cascade with an M(s) and that the system will be controlled by the loop shown in Figure 10.20, where G(s) = M(s)P(s) and H = 1. For each M(s) that follows, draw the Nyquist diagram when K = 1, and find the range of closed-loop stability for K > 0.

a. 

M(s) = -K

b.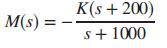 

c. 

Compare your results with those obtained in Problem 47, Chapter 8.

                                         

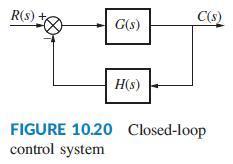
K(s + 200) M(s) = s+ 1000