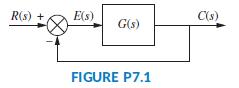
Question: The parabolic trough collector (Camacho, 2012) is embedded in a unit feedback configuration as shown in Figure P7.1, where G(s) = GC(s)P(s) and a. Assuming
The parabolic trough collector (Camacho, 2012) is embedded in a unit feedback configuration as shown in Figure P7.1, where G(s) = GC(s)P(s) and
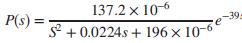
a. Assuming GC(s) = K, find the value of K required for a unit-step input steady-state error of 3%. Use the result you obtained in Problem 70, Chapter 6, to verify that the system is closed-loop stable when that value of K is used.
b. What is the minimum unit-step input steady-state error achievable with GC(s) = K?
c. What is the simplest compensator, GC(s), that can be used to achieve a steady-state error of 0%?
Data From Problem 70, Chapter 6:
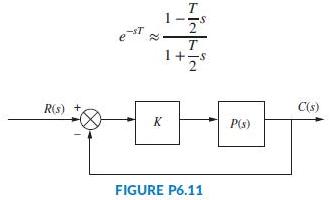
The fluid temperature of a parabolic trough collector (Camacho, 2012) will be controlled by using a unity feedback structure as shown in Figure P6.11. Assume the open-loop plant transfer function is given by

Use the Routh-Hurwitz criteria to find the range of gain K that will result in a closed-loop stable system.
Note: Pure time-delay dynamics, such as the one in the transfer function of the parabolic trough collector, cannot be treated directly using the Routh-Hurwitz criterion because it is represented by a non rational factor. However, a Padé approximation can be used for the non rational component. The Padé approximation was introduced in Problem 6.61, but it can appear in different forms. Here, it is suggested you use a first-order approximation of the form
137.2 x 106 P(s) = S + 0.0224s + 196 x 10-6 e 39.
Step by Step Solution
3.37 Rating (169 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


