Mara Faccio is considering investing in the common stock of Merville Enterprises. In addition, Mara will either borrow or lend at the risk-free rate. The relevant parameters are:

Suppose Mara chooses to invest a total of $1,000, $350 of which is to be invested in Merville Enterprises and $650 will be invested in the risk-free asset. The expected return on her total investment is a weighted average of the two returns:

Because the expected return on the portfolio is a weighted average of the expected return on the risky asset (Merville Enterprises) and the risk-free return, the calculation is analogous to the way we treated two risky assets. In other words, Equation 11.4 applies here.

Using Equation 11.5, the formula for the variance of the portfolio can be written as:

The relationship between risk and expected return for portfolios composed of one risky asset and the riskless asset can be seen in Figure 11.8. Mara’s choice of portfolio between the two assets is represented by a straight line between the risk-free rate and a pure investment in Merville Enterprises. Unlike the case of two risky assets, the opportunity set is straight, not curved.

Suppose that, alternatively, Mara borrows $200 at the risk-free rate. Combining this with her original sum of $1,000, she invests a total of $1,200 in Merville. Her expected return would be:

Here, she invests 120 percent of her original investment of $1,000 by borrowing 20 percent of her original investment. Note that the return of 14.8 percent is greater than the 14 percent expected return on Merville Enterprises. This occurs because she is borrowing at 10 percent to invest in a security with an expected return greater than 10 percent.

The standard deviation is:

Figure 11.8 Relationship between Expected Return and Risk for Portfolios Composed of the Riskless Asset and One Risky Asset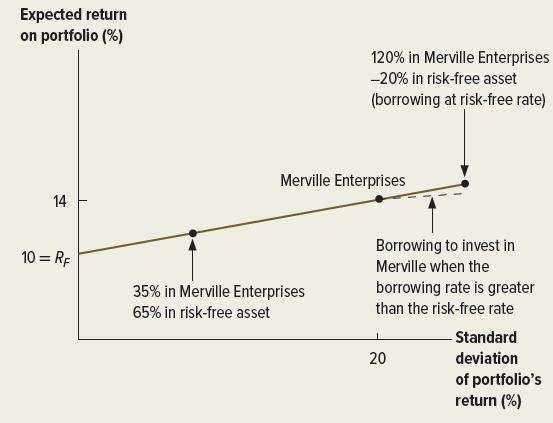

The standard deviation of 24 percent is greater than 20 percent, the standard deviation of the Merville investment, because borrowing increases the variability of the investment. This investment also appears in Figure 11.8.

So far, we have assumed that Mara is able to borrow at the same rate at which she can lend.8 Now let us consider the case where the borrowing rate is above the lending rate. The dotted line in Figure 11.8 illustrates the opportunity set for borrowing opportunities in this case.

The dotted line is below the solid line because a higher borrowing rate lowers the expected return on the investment.

Transcribed Image Text:

Expected return Standard deviation Common Stock of Merville 14% 20 Risk-Free Asset 10% 0