The Physical Bank of New York has the following market value balance sheet:

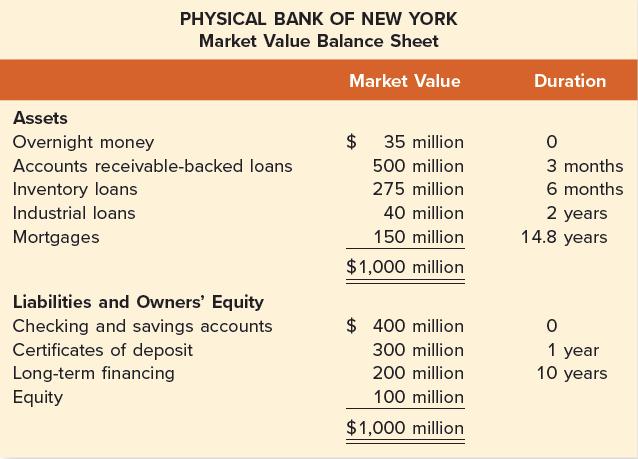
The bank has $1,000 million of assets and $900 million of liabilities. Its equity is the difference between the two: $100 million ( = $1,000 million − 900 million ) . Both the market value and the duration of each individual item are provided in the balance sheet. Both overnight money and checking and savings accounts have a duration of zero. This is because the interest paid on these instruments adjusts immediately to changing interest rates in the economy.

The bank’s managers think that interest rates are likely to move quickly in the coming months. Because they do not know the direction of the movement, they are worried that their bank is vulnerable to changing rates. They call in a consultant, James Charest, to determine a hedging strategy.

James first calculates the duration of the assets and the duration of the liabilities: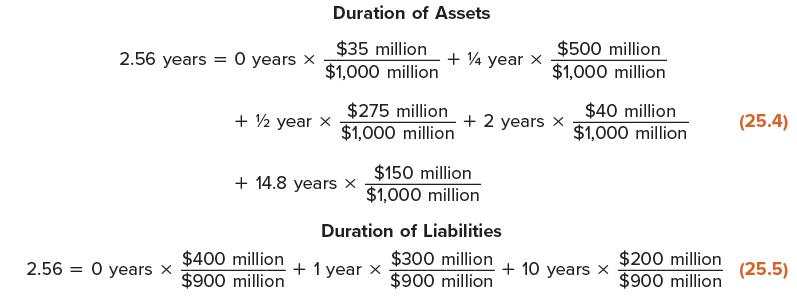

The duration of the assets, 2.56 years, equals the duration of the liabilities. Because of this, James argues that the firm is immune to interest rate risk.

To be on the safe side, the bank calls in a second consultant, Gail Ellert. Gail argues that it is incorrect to match durations because assets total $1,000 million and liabilities total only $900 million. If both assets and liabilities have the same duration, the price change on a dollar of assets should be equal to the price change on a dollar of liabilities. However, the total price change will be greater for assets than for liabilities because there are more assets than liabilities in this bank. The firm will be immune to interest rate risk only when the duration of the liabilities is greater than the duration of the assets. Gail states that the following relationship must hold if the bank is to be immunized—that is, immune to interest rate risk: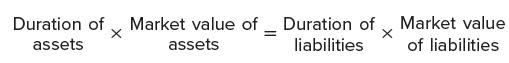

She says that the bank should not equate the duration of the liabilities with the duration of the assets. Rather, using Equation 25.6, the bank should match the duration of the liabilities to the duration of the assets. She suggests two ways to achieve this match.

1. Increase the duration of the liabilities without changing the duration of the assets. Gail argues that the duration of the liabilities could be increased to: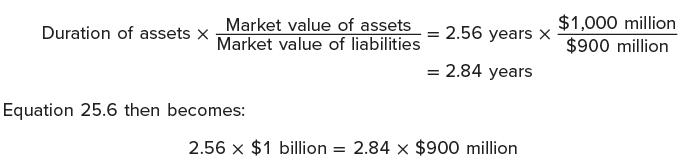

2. Decrease the duration of the assets without changing the duration of the liabilities. Alternatively, Gail points out that the duration of the assets could be decreased to:

Transcribed Image Text:

PHYSICAL BANK OF NEW YORK Market Value Balance Sheet Assets Overnight money Accounts receivable-backed loans Inventory loans Industrial loans Mortgages Liabilities and Owners' Equity Checking and savings accounts Certificates of deposit Long-term financing Equity Market Value $ 35 million 500 million 275 million 40 million 150 million $1,000 million $400 million 300 million 200 million 100 million $1,000 million Duration 0 3 months 6 months 2 years 14.8 years 0 1 year 10 years