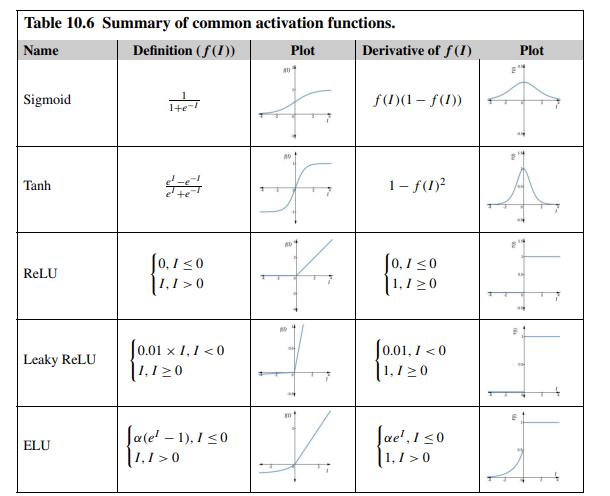
a. Derivatives of various activation functions. Show how the derivatives of activation functions, including sigmoid, tanh, and ELU in Table 10.6, are derived in mathematical details.

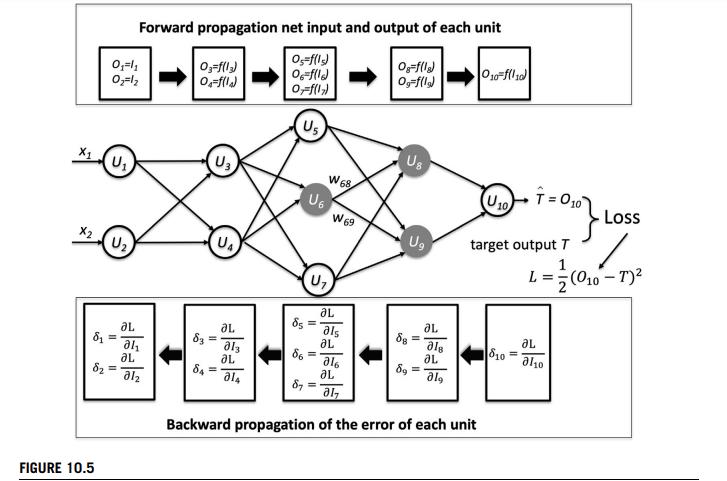
b. Backpropagation algorithm. Consider a multilayer feed-forward neural network as shown in Fig. 10.5 with sigmoid activation and mean-squared loss function $L$. Prove (1) Eq. (10.3) for computing the error in the output unit $\left({\delta }_{10}\right)$; (2) Eq. (10.4) for computing the errors in hidden units ${\delta }_9$ and ${\delta }_6$; (hint: consider the chain rule); and (3) Eq. (10.5) for updating weights (hint: consider the derivative of the loss with respect to weights).

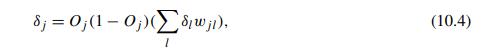
c. Relation between different activation functions. Given the sigmoid function $\sigma \left(I\right)=$ $\frac{1}{1+e^{-I}}$ and hyperbolic tangent function $\tanh \left(I\right)=\frac{e^I-e^{-I}}{e^I+e^{-I}}$, show in mathematics how $\tanh \left(I\right)$ can be transformed from sigmoid through shifting and re-scaling.

Transcribed Image Text:

8j = 0j (10;)(0; Tj), (10.3)