Given \(n\) training examples \(\left(\mathbf{x}_{i}, y_{i}ight)(i=1,2, \ldots, n)\) where \(\mathbf{x}_{i}\) is the feature vector of \(i\) th training example and \(y_{i}\) is its label, we training an support vector machine (SVM) with Radial Basis Function (RBF) kernel on the training data. Note that the RBF kernel is defined as \(K_{\mathrm{RBF}}(\mathbf{x}, \mathbf{y})=\) \(\exp \left(-\gamma\|\mathbf{x}-\mathbf{y}\|_{2}^{2}ight)\).

a. Let \(\mathbf{G}\) be the \(n \times n\) kernel matrix of RBF kernel, i.e. \(\mathbf{G}[i, j]=K_{\mathrm{RBF}}\left(\mathbf{x}_{i}, \mathbf{x}_{j}ight)\). Prove that all eigenvalues of \(\mathbf{G}\) are nonnegative.

b. Prove that RBF kernel is the sum of infinite number of polynomial kernels.

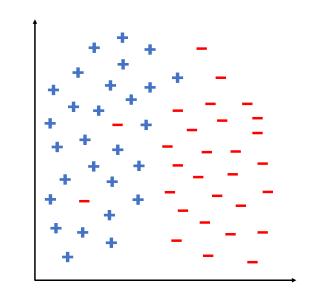
c. Suppose the distribution of training examples is shown in Fig. 7.30, where "+" denotes positive example and "_" denotes the negative sample. If we set \(\gamma\) large enough (say 1000 or larger), what could possibly be the decision boundary of the SVM after training? Please draw it on Fig. 7.30.

d. If we set \(\gamma\) to be infinitely large, what could possibly happen when training this SVM?

Fig. 7.30

Transcribed Image Text:

+