A floating-point number is a pair, (m, d), of integers, which represents the number m × bd, where b is either 2 or 10. In any real-world programming environment, the sizes of m and d are limited; hence, each arithmetic operation involving two floating-point numbers may have some roundoff error. The traditional way to account for this error is to introduce a machine precision parameter, ε

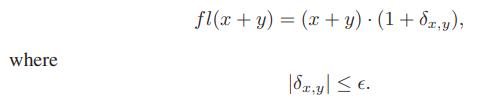
Suppose we are given a set of positive floating-point numbers, {x₁, x₂,...,x_n}, and we wish to sum up all these numbers. Any such summation algorithm can be modeled with a binary expression tree, T, that has each xi associated with one of its external nodes, with each internal node, v, representing the floatingpoint sum of the floating point numbers computed by v’s children. Given the machine-precision approach to bounding floating-point errors, and assuming that ε is small enough so that ε² times any floating-point number is negligibly small, then we can use a term, en, to estimate an upper bound for the roundoff error for summing these numbers using the tree T as

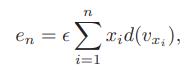
where v_xi is the external node associated with xi and d(v_xi) is the depth of this node in T. Design an efficient algorithm for constructing the binary expression tree, T, that minimizes en. What is the running time of your method?

fl(x + y) = (x + y) - (1+ 8r,y), where