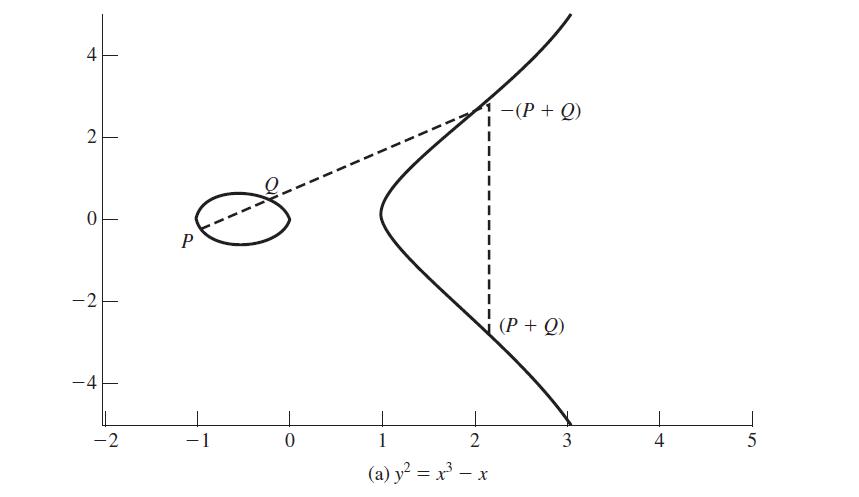
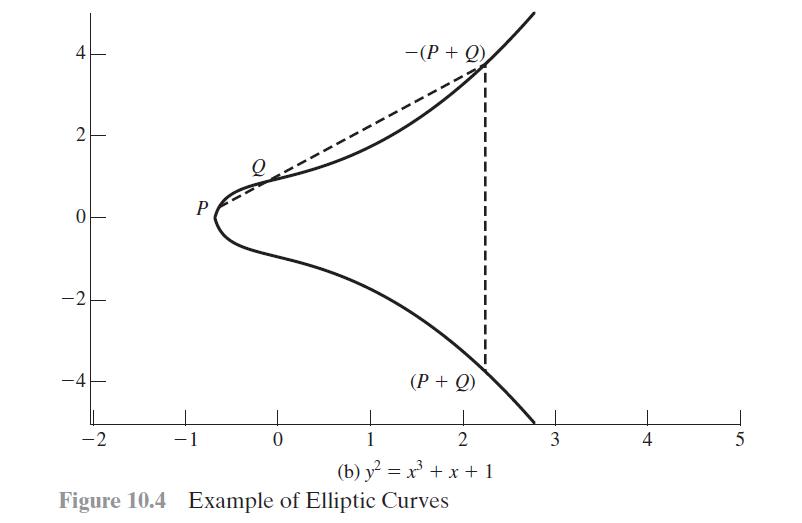
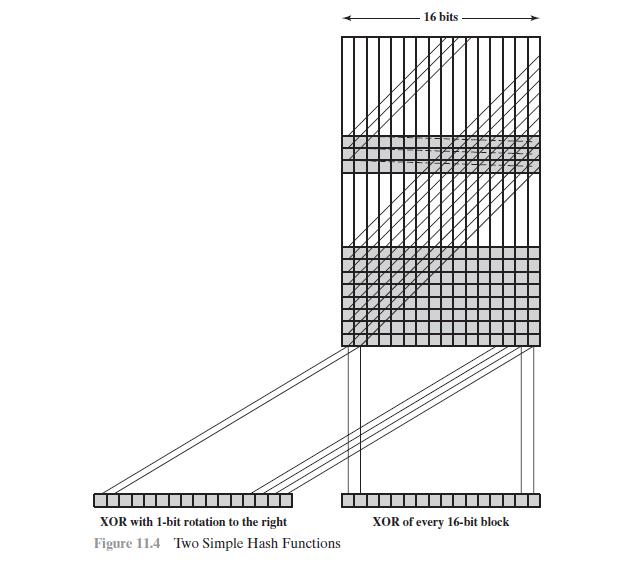
Cryptography And Network Security 5th Edition William Stallings - Solutions
Discover comprehensive resources for "Cryptography and Network Security, 5th Edition" by William Stallings. Access an online answers key and solution manual with detailed solutions in PDF format. Explore solved problems and step-by-step answers for each chapter, offering a valuable test bank for students and instructors alike. Dive into the instructor manual, providing insights and answers to textbook questions and answers, all available for free download. Enhance your understanding with chapter solutions and ensure success with this essential guide to cryptography and network security concepts.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()