The problem of accurately summing a set S of n floating-point numbers, S = {x₁, x₂,...,x_n}, on a real-world computer is more challenging than might first appear. For example, using the standard accumulating-sum algorithm to compute the harmonic numbers, 

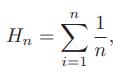
in floating-point produces a sequence that converges to a constant instead of growing to infinity as a function close to ln n. This phenomenon is due to the fact that floating-point addition can suffer from round-off errors, especially if the two numbers being added differ greatly in magnitude. Fortunately, there are several useful heuristic summation algorithms for dealing with this issue, with one of them being the following. Let xi and xj be two numbers in S with smallest magnitudes. Sum xi and xj and return the result to S. Repeat this process until only one number remains in S, which is the sum. This algorithm will often produce a more accurate sum than the straightforward summation algorithm, because it tends to minimize the round-off errors of each partial sum. Describe how to implement this floating-point summation algorithm in O(n log n) time. 

Transcribed Image Text:

n Hn n i=1