Question: Without using calculus (as in the previous exercise), show that, if n is a power of 2 greater than 1, then, for H n ,

Without using calculus (as in the previous exercise), show that, if n is a power of 2 greater than 1, then, for Hn, the nth harmonic number, 

Hn ≤ 1 + Hn/2

Use this fact to conclude that Hn ≤ 1 + [log n], for any n ≥ 1.


Data From Previous Exercise

Use the fact that, for a decreasing integrable function, f,

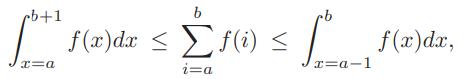
cb+1 b f(x)dx < f (x)dx, r=a r=a-1 2=a 

to show that, for the nth harmonic number, Hn, 

ln n ≤ Hn ≤ 1 + ln n.

cb+1 b f(x)dx < f (x)dx, r=a r=a-1 2=a

Step by Step Solution

★★★★★

3.37 Rating (156 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

If n is a power of 2 greater than 1 then there are n2 terms in the differe... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Data Structures Algorithms Questions!

Q:

Using the definition of a c-incremental algorithm from the previous exercise, show that, if a c-incremental algorithm A has a worst-case running time t(N) in the RAM model, as a function of the...

Q:

Consider the previous exercise, but suppose the city of Irvine, California, changed its dog-owning ordinance so that it still allows for residents to own a maximum of three dogs per household, but...

Q:

Solve the previous exercise using a queue instead of stack. That is, suppose you are given an array, A, containing n numbers in order, as in the previous exercise. Describe in pseudocode an efficient...

Q:

Previous Exercise: C-3.12 Without using calculus (as in the previous exercise), show that, if n is a power of 2 greater than 1, then, for Hn, the nth harmonic number, Use this fact to conclude that...

Q:

Can anyone help me with this question about bounding summation? Without using calculus (as in the previous exercise), show that, if n is a power of 2 greater than 1, then, for H_n, the nth harmonic...

Q:

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

Q:

Create a Recursion Class that will implement the following recursive algorithms: Implement a recursive algorithm to compute the n th Harmonic number defined as: H n = k=1 n 1 k where k is a natural...

Q:

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

Q:

Math assignment show all work . 10. Solve by the method of false position: A quantity and its 2/3 are added together and from the sum 1/3 of the sum is subtracted, and 10 remains. What is the...

Q:

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

Q:

What effect does leasing have on the stability of a firms reported earnings?

Q:

On the first day of the fiscal year, a delivery truck with a list price of $86,500 was acquired in exchange for an old delivery truck and $75,000 cash. The old truck had a book value of $15,675 at...

Q:

A lawsuit in progress against a company is an example of a blank blank that needs to be considered when completing an audit

Q:

12. The IRS maintains a section called Tax Pro News and Events. Locate this Web site and print out the first page of the first item appearing on Tax Pro News and Events.

Q:

Give a complete justification of Proposition 12.1.

Q:

Show that the nodes of any AVL tree T can be colored red and black so that T becomes a red-black tree.

Q:

The boolean indicator used to mark nodes in a red-black tree as being red or black is not strictly needed when we have distinct keys. Describe a scheme for implementing a red-black tree without...

Q:

Bellwood Corp. is comparing two different capital structures. Plan I would result in 32,000 shares of stock and $94,500 in debt. Plan II would result in 26,000 shares of stock and $283,500 in debt....

Q:

Dillon Labs has asked its financial manager to measure the cost of each specific type of capital as well as the weighted average cost of capital. The weighted average cost is to be measured by using...

Q:

Say your income is $ 1 0 0 K . Given the following tax brackets, what is your effective tax rate? Taxrate Taxable Income ( Single ) . 1 0 % 1 2 % $ 1 1 , 0 0 1 to $ 4 4 , 7 2 5 $ 4 4 , 7 2 6 to $ 9 5...