Specify, design, and implement a class that can be used to simulate a lunar lander, which is a small spaceship that transports astronauts from lunar orbit to the surface of the moon. When a lunar lander is constructed, the following items should be initialized as follows:

(1). Current fuel flow rate as a fraction of the maximum fuel flow (initially zero)

(2). Vertical speed of the lander (initially zero meters/sec)

(3). Altitude of the lander (specified as a parameter of the constructor)

(4). Amount of fuel (specified as a parameter of the constructor)

(5). Mass of the lander when it has no fuel (specified as a parameter of the constructor)

(6). Maximum fuel consumption rate (specified as a parameter of the constructor)

(7). Maximum thrust of the lander’s engine (specified as a parameter of the constructor)

The lander has accessor methods that allow a program to retrieve the current values of any of the preceding seven items. There are only two modification methods, described next. The first modification method changes the current fuel flow rate to a new value ranging from 0.0 to 1.0. This value is expressed as a fraction of the maximum fuel flow.

The second modification method simulates the passage of a small amount of time. This time, called t, is expressed in seconds and will typically be a small value such as 0.1 seconds. The method will update the first four values in the preceding list to reflect the passage of t seconds. To implement this method, you will require a few physics formulas, listed below. These formulas are only approximate because some of the lander’s values are changing during the simulated time period. But if the time span is kept short, these formulas will suffice.

Fuel flow rate: Normally, the fuel flow rate does not change during the passage of a small amount of time. But there is one exception: If the fuel flow rate is greater than zero and the amount of fuel left is zero, then you should reset the fuel flow rate to zero
(because there is no fuel to flow).

Velocity change: During t seconds, the velocity of the lander changes by approximately this amount (measured in meters/sec):

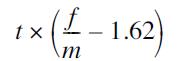
The value m is the total mass of the lander, measured in kilograms (i.e., the mass of a lander with no fuel plus the mass of any remaining fuel). The value f is the thrust of the lander’s engine, measured in newtons. You can calculate f as the current fuel flow rate times the maximum thrust of the lander. The number –1.62 is the downward acceleration from gravity on the moon.

Altitude change: During t seconds, the altitude of the lander changes by t × c meters, where v is the vertical velocity of the lander (measured in meters/ sec with negative values downward).

Change in remaining fuel: During t seconds, the amount of remaining fuel is reduced by t × r × c kilograms. The value of r is the current fuel flow rate, and c is the maximum fuel consumption (measured in kilograms per second).

We suggest that you calculate the changes to the four items in the order just listed. After all the changes have been made, there are two further adjustments. First, if the altitude has dropped below zero, then reset both altitude and velocity to zero (indicating that the ship has landed). Second, if the total amount of remaining fuel drops below zero, then reset this amount to zero (indicating that we have run out of fuel).

Transcribed Image Text:

L-1.62) tx