This project is a continuation of the previous project. For a quadratic expression such as ax² + bx + c, a real root is any double number x such that ax² + bx + c = 0. For example, the quadratic expression 2x² + 8x + 6 has one of its real roots at x= -3 because substituting x= -3 in the formula 2x² + 8x + 6 yields the value:

2 × (–3² ) + 8 × (–3) + 6 = 0

There are six rules for finding the real roots of a quadratic expression:

(1). If a, b, and c are all zero, then every value of x is a real root.

(2). If a and b are zero but c is nonzero, then there are no real roots.

(3). If a is zero and b is nonzero, then the only real root is x = -c/b.

(4). If a is nonzero and b² < 4ac, then there are no real roots.

(5). If a is nonzero and b² = 4ac, then there is one real root, x = -b/2a.

(6). If a is nonzero and b² > 4ac, then there are two real roots:

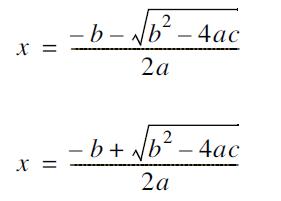
Write a new method that returns the number of real roots of a quadratic expression. This answer could be 0, 1, 2, or infinity. In the case of an infinite number of real roots, have the method return 3. (Yes, we know that 3 is not infinity, but for this purpose it is close enough!) Write two other methods that calculate and return the real roots of a quadratic expression. The precondition for both methods is that the expression has at least one real root. If there are two real roots, then one of the methods returns the smaller of the two roots, and the other method returns the larger of the two roots. If every value of x is a real root, then both methods should return zero.

Data from Previous Project

A one-variable quadratic expression is an arithmetic expression of the form , where ax², bx, and c are some fixed numbers (called the coefficients) and x is a variable that can take on different values. Specify, design, and implement a class that can store information about a quadratic expression. The constructor should set all three coefficients to zero, and another method should allow you to change these coefficients. There should be accessor methods to retrieve the current values of the coefficients. There should also be a method to allow you to “evaluate” the quadratic expression at a particular value of x (i.e., the method has one parameter x and returns the value of the expression ax² + bx + c).

Also write the following static methods to perform these indicated operations:

public static Quadratic sum(
Quadratic q1,
Quadratic q2
)
// Postcondition: The return value is the
// quadratic expression obtained by adding
// q1 and q2. For example, the c coefficient
// of the return value is the sum of q1’s c
// coefficient and q2’s c coefficient.
public static Quadratic scale(
double r,
Quadratic q
)
// Postcondition: The return value is the
// quadratic expression obtained by
// multiplying each of q’s
// coefficients by the number r.

The first argument of the scale method is a double number (rather than a quadratic expression). For example, this allows the method activation Quadratic.scale(3.14, q) where q is a quadratic expression.

Transcribed Image Text:

-b- Nb² - 4ac x = 2a - b+ b?. 4ас 2a II