This project requires a little understanding of velocity and gravity, but don’t let that scare you away! It’s actually an easy project. The assignment is to write a class in which each object represents a satellite in orbit around the Earth’s equator. Each object has four instance variables. 

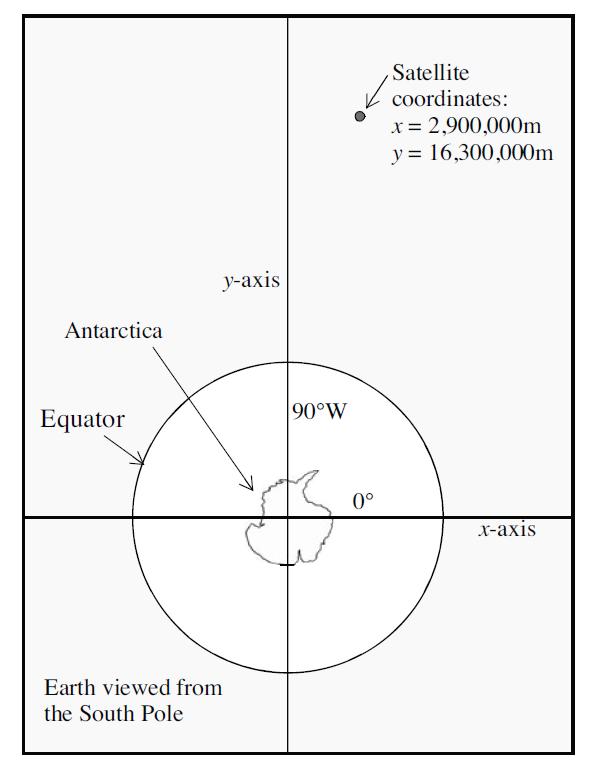
Two variables store the current x and y positions of the satellite in a coordinate system with the origin at the center of the Earth. The plane formed by the xand y-axes comes out through the equator, with the positive x-axis passing through the equator at the Greenwich prime meridian. The positive y-axis is 90 degrees away from that, at the 90°W meridian, and all measurements are in meters. The drawing in the next column shows a possible location of the satellite as viewed from far above the South Pole.

Two other variables (vx and vy) store the current velocity of the satellite in the x and y directions. These measurements are in meters per second. The values can be positive (which means that the satellite is moving toward the positive direction of the axis) or negative (which means that the satellite is moving toward the negative axis).

Your class should have methods to set and retrieve all four instance variables. Also include a modification method that will change all four instance variables to reflect the passage of a small amount of time t (measured in seconds). When t is small, the equations for the new values of x, y, vx, and vy are given by:

new value of x = x + vx*t

new value of y = y + vy*t

new value of vx = vx + ax*t

new value of vy = vy + ay*t.

The numbers ax and ay are the current accelerations from gravity along the x- and y-axes, determined by:

ax = –G*M*x/d³

ay = –G*M*y/d³

G = gravitational constant in N-m²/sec²

    = 6.67 x 10^-11

M = mass of the Earth in kilograms

    = 5.97 x 10²⁴

d = distance of the satellite from center of Earth

   = √x² + y²

Include accessor methods to retrieve the current values of ax, ay, d, and the satellite’s current altitude above the surface of the Earth (the value of d minus the equatorial radius of the Earth, which is about 12,756,300 meters).

Include a boolean method that determines whether the satellite has crashed into the Earth. For the method that simulates the passage of a small amount of time, there should be a check to see whether the satellite has crashed into the surface of the Earth. If so, the method should set both velocities to zero and not change the x and y locations. Of course, all of this ignores many factors (such as air resistance when the satellite approaches the Earth’s atmosphere).

Use your satellite class in a small application program that allows the user to set the initial values of x, y, vx, and vy. The program then simulates the satellite’s flight by repeatedly calling the simulation method with t = 1. The program’s output consists of a list of the x, y, vx, and vy values printed once every 60 simulated seconds (with the total amount of time simulated being specified by the user).

You can run your program using some actual values that are similar to Canada’s Alouette I satellite,
launched in 1962:

Initial x = 7,392,000 meters

Initial y = 0

Initial vx = 0

Initial vy = 7,349 meters/sec

Each complete orbit should take a bit more than 106 minutes.

Transcribed Image Text:

Satellite coordinates: x = 2,900,000m y = 16,300,000m у-ахis Antarctica 90°W Equator 0° х-ахis Earth viewed from the South Pole