Suppose that we are fitting the straight line y = 0 + 1 x +

Suppose that we are fitting the straight line y = β₀ + β₁x + ∈, but the variance of the y's now depends on the level of x; that is,

 

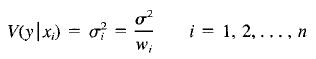
where the w, are known constants, often called weights. Show that if we choose estimates of the regression coefficients to minimize the weighted sum of squared errors given by

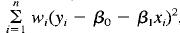
the resulting least squares normal equations are =

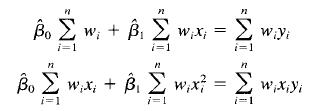
Transcribed Image Text:

Vy|x) = o? W; i = 1, 2, ... , n