(a) The transfer function for the right-side rectangular-rule integrator was found in Problem 2.2-1 to be Y(z)/X(z)...
Question:
(a) The transfer function for the right-side rectangular-rule integrator was found in Problem 2.2-1 to be Y(z)/X(z) = Tz/(z −1) . We would suspect that the reciprocal of this transfer function should yield an approximation to a differentiator. That is, if w(kT) is a numerical derivative of x(t) at t = kT,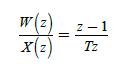
Write the difference equation describing this differentiator.
(b) Draw a figure similar to those in Fig. P2.2-1 illustrating the approximate differentiation.
(c) Repeat part (a) for the left-side rule, where W(z)/X(z) = T / (z −1).
(d) Repeat part (b) for the differentiator of part (c).
Problem 2
The trapezoidal rule (modified Euler method) for numerical integration approximates the integral of a function x(t) by summing trapezoid areas as shown in Fig. P2.2-2. Let y(t) be the integral of x(t) .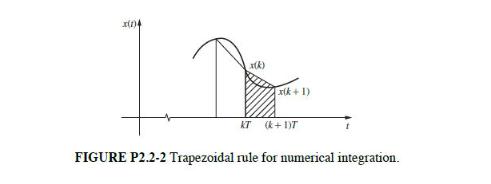
Step by Step Answer:

Digital Control System Analysis And Design
ISBN: 9780132938310
4th Edition
Authors: Charles Phillips, H. Nagle, Aranya Chakrabortty





